Legitimate QIP and improvement half-life

Using improvement half-life to predict future targets and time required

A legitimate QIP is a process that achieves a benchmark rate of continuous improvement. Most goals lack specificity; they fail to define both a rational objective and a time line for its achievement. What is needed is an empirically based goal-setting model for legitimate quality improvement process (QIP) activities. A legitimate QIP is a process that achieves a benchmark rate of continuous improvement.

Any defect level, subject to legitimate QIP, decreases at a constant rate, so that when plotted on semi-log paper against time, it falls on a straight line. Hence, it is easy to extrapolate. The word DEFECT is used in a general sense, which includes errors, rework, yield loss, unnecessary reports, cycle times (manufacturing, design, administrative etc), unscheduled downtime, inventory, employee turnover, absenteeism, lateness, unrealized human potential, accidents, late deliveries, order lead time, setup time, cost of poor quality, and warranty costs.

Specific goals (SMART) should be set based on knowledge of the means that will be used to achieve them. Yet the means are rarely known at the time goals are set. The usual result is that if the goal is too low, we will underachieve relative to our potential. If the goal is too high, we will underperform relative to others' expectations. What is really needed to set rational goals is a means of predicting what is achievable if some sort of standard means for improvement were used.

For each increment in time that is equal to the half-life, the defect level drops, on average, by 50%. When talking about defects of errors, the minimum is potentially zero. The difference between current performance and the achievable minimum is a mathematical generalization of waste. The model is that for each increment in time that is equal to the half-life, the defect level drops, on average, by 50%.

For example, if the initial defect level was 10% and the the defect half-life was six months, then after the first six months, the defect level would be down to 5%, after the next six months, 2.5%, and so on. A large value for the number of IMPROVEMENT CYCLES indicates a mature project, while a small value is indicative of a start-up effort. Projects can be grouped into three types, with increasing half-lives:

  1. UNI-FUNCTIONAL: projects within a single organizational function as measured by the team's ability to autonomously solve, approve, and implement.
    Half-life range: 0~6 months, average 3 months.
  2. CROSS-FUNCTIONAL: involving different departments (e.g. marketing, design, purchasing, manufacturing, quality assurance, and sales. From a traditional perspective there might be functional winners and losers in the solving of the problem. These internal trade-offs are weighed against the entire organization's commitment to improved value to its customers. The consensus building required to achieve a solution could be expected to add time — particularly in organizations that are large, bureaucratic, or both — to the problem-solving process.
    Half-life range: 6~12 months, average 9 months.
  3. CROSS-ENTITY: These involve different business entities: the problem-solving team and its external customers or suppliers. Action must result from negotiation, which adds further to the time for improvement.
    Half-life range: 12~24 months, average 18 months.

Practice Question

GM’s order-to-delivery cycle was 54 days in 2000. GM cut their order-to-delivery cycle by 50% by 2004. Their goal is an order-to-delivery cycle of 7-10 days. How many periods are needed to achieve the goal?

  1. Use the first method above to "calculate improvement half-life" using [ Y0 ] = 54, [ Y ] = 27, and [ t ] = 4.
    Result = 4.
    [Interpretation]: the half-life of quality improvement (time for the problem to decrease by 50%) is 4 and the unit is "years" since that is the unit used for [ Y0 ] and [ Y ], hence [ t½ ] is 4 "years".
  2. Use the third method above to "predict time to reach specified target" using [ Y0 ] = 27, [ t½ ] = 4, [ Y ] = 10, and [ Ymin ] = 7.
    Result = 10.95 (2.7 cycles).
    [Interpretation]: this is an example where the "ultimate goal" can not be reduced to zero, so we take the lower limit of the target range (7~10) as the maximum achievable value, that is, 7;
  3. Then take the upper limit of that range, that is, 10, as the earliest time that the target has been reached, and then calculate the result. The calculated result shows that
    1. the time required to reach this level is 10.95 years at the earliest
    2. the number of improvement cycles required is at least 2.7 cycles
    With each quality improvement cycle having the same length as the improvement half-life, this means that the earliest the goal would be achieved is the year 2016 [starting from the year 2004 when the starting level was 27, and adding on 3 cycles (2.7) of 4 years, that is 12 years].

Try It Yourself!

In the three examples below, the level of "defects" is used, therefore the value is higher before improvement than after improvement. Consequently, the results for half-life and other time parameters are positive (greater than zero).

The opposite is also possible: process compliance can be improved from a lower percentage to a higher one. These same equations can be used for the calculations, but the results will be negative (below zero).

If values for improvement are expressed as a percentage (for example, 4.5%), input the number without the percentage symbol (for example, 4.5) or as a decimal (for example, 0.045). Make sure that whichever method you use to input data is consistent throughout; for example 4.5% down to 2.3% entered as either [4.5 and 2.3] or [0.045 and 0.023].

The unit of time depends on the user: for example, whether you use day, month, or year, whichever one you use for data entry will also be the unit for the computed answer.

Excel spreadsheet
Put data into {data} cells in column B;
for each calculation, put its equation (from below) into the appropriate cell of the three cells with {data/eqn},
and data into the other two {data/eqn} cells
  A B C
1 Y {data/eqn} "target reached" or "expected result" after specified time period [t-t0]
2 Y0 {data} "current defect level" at time t0
3 Ymin {data} The "ultimate goal" is the maximum improvement possible. For reducing defects, this will be zero; however, some processes have an achievable goal that is not zero.
4 ln(2) 0.69315  
5 t {data/eqn} total time required for the future/desired target [ Y ] to be reached. [t-t0] is the time taken to achieve the improvement from BEFORE and AFTER implementing change.
6 t0 {data} starting point of improvement program (usually set to zero in calculations)
7 t½ {data/eqn} current half-life (time required to improve by 50%)

① Calculate improvement half-life {B7}

Use the results BEFORE and AFTER improvement, together with the TIME taken to achieve that improvement, to calculate the half-life (time required to improve by 50%).

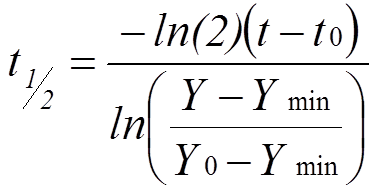
half-life equation

The half-life [ t½ ] units are the same as the units for time input in [ t ]; for example, if [ t ] is in "days", then the half-life [ t½ ] is calculated in "days".
Use t0 = 0 in the equation.

EXCEL:
t½ = -B4*(B5-B6)/LN((B1-B3)/(B2-B3))

 



② Predict result {B1}

Using the current half-life, input the project time frame and calculate the expected result.

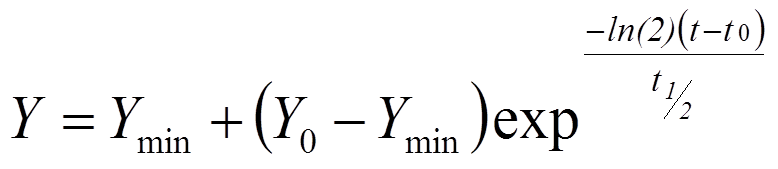
half-life equation
  • The "ultimate goal" [ Ymin ] is the maximum improvement possible.
    For many projects working on reducing defects, this will be zero; however, some processes have an achievable goal that is not zero, such as time waiting to see a doctor in outpatients or number of prescriptions processed each day.
  • The units for the "target reached" [ Y ] are the same as the units for "current defect level" [ Y0 ] and "ultimate goal" [ Ymin ].
  • Use t0 = 0 in the equation.
EXCEL:
Y = B3+(B2-B3)*EXP(-B4*(B5-B6)/B7)

 



③ Predict time {B5}

Using the current half-life, input the desired target to predict the time required to reach it. Also, convert that time period into the number of QIP cycles required.

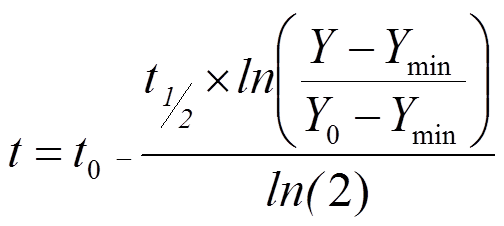
half-life equation

Time required [ t ] units are the same as the units for half-life input in [ t½ ]; for example, if [ t½ ] is in "days", then the time required [ t ] is calculated in "days".

Use t0 = 0 in the equation.

EXCEL:
t = B6-(B7*LN((B1-B3)/(B2-B3))/B4)

 



References:

  1. Anderson C. How Much Time Is Needed for Process Improvement?
    [www.bizmanualz.com]
  2. Schneiderman AM. Setting quality goals
    American Society for Quality Control, 1988; April: 51-7. (PDF:72KB)
    [www.schneiderman.com]
  3. Schneiderman AM. Origin of Schneiderman's Half-life Method
    [www.schneiderman.com]
  4. Schneiderman AM. Are There Limits to Total Quality Management?
    [www.schneiderman.com]