公認的QIP

以品質改善半衰期預測未來的結果、所需的時間

公認的品質改善流程(QIP)：持續達到基準變化率。 常見的目標缺乏具體性：都沒有考慮到目的值的合理性或其達成的期限。所需要的是用於公認品質改進過程（QIP）活動的基於憑經驗驗證的目標設定模型。公認的品質改善流程(QIP)：持續達到基準變化率。

任何缺陷情況，經過認可的品質改善作業，以一定的速度減少，如此在半對數坐標紙上與時間，會落在一個直線上。因此，很容易推論。〝缺陷〞這個字用在一般的意思，包括錯誤、重做、產量損失、不必要的報告、循環時間﹝製造、設計、管理等﹞、非計畫停機、庫存量、員工流動率、曠職、遲到、未實現的人為潛能、意外、延遲交貨、訂貨與交貨相隔的時間、準備時間、不良品質成本與保固成本。

具體的目標﹝SMART﹞應該確認可利用的資源後才進行設置。然而在擬訂目標時很少澄清資源。結果，通常是兩個極端之一：如果目標太低，我們將差生相對於我們的潛力；如果目標太高，我們將弱於別人的期望。為了設置合理的目標，需要一個可靠達到改進的機制來應用其成果預測未來可實現的目標。

每個半衰期，缺陷平均會下降一半。 談到錯誤的缺陷，最佳的可能性為缺陷零。衡量在當前的成效與可達到的最小值之差距可數字化「浪費」。每半衰期，缺陷平均就會下降 50%。

例如，如果開始的缺陷為 10% 且缺陷半衰期為半年，那麼第一個半年後，缺陷將下調至5%，次六個月內，會下降至 2.5% 等等。改善週期的次數多表示一個成熟的專案，週期次數少表示沒有啟動多久。專案可分為以下三類，越往下半衰期越久：

  1. 同群組的問題：由群組自主解決、審批與實施解決方案來證明作業的自主權。
    半衰期範圍：0~6 月，平均 3 月。
  2. 跨單位：涉及到不同部門﹝如行銷、設計、採購、品質保證與銷售﹞。從傳統的角度來看也許有利於某些單位﹝贏家﹞，而不利於其他單位﹝輸家﹞。這些內部交易權衡機構對改善客戶服務的承諾。實現解決方案所需的共識會增加時間 — 特別是在機構內大、官僚或者兩個都是。
    半衰期範圍：6~12 月，平均 9 月。
  3. 跨機構問題：涉及到不同機構：問題解決團隊與外部顧客或供應商。必須協商後才動作，此會增加了達成改善需要的時間。
    半衰期範圍：12~24 月，平均 18 月。

實踐題

通用汽車的訂單到交貨週期在 2000 年為 54 天，到了 2004 年通用汽車公司削減了訂單到交貨週期幅度為50％。他們的目標是訂單到交貨週期在 7~10 天範圍內。需要多少時間來實現這一目標？

  1. 以 [ Y0 ] = 54, [ Y ] = 27 和 [ t ] = 4 使用上述「半衰期計算公式」來計算改善半衰期。
    結果 = 4。
    解釋：品量改進的半衰期（減少 50％）為 4，且因為 [ Y0 ] 和 [ Y ] 的單位為〝年〞，從而 [ t½ ] 為 4 〝年〞。
  2. 以 [ Y0 ] = 27, [ t½ ] = 4, [ Y ] = 10 和 [ Ymin ] = 7 使用上述「預測所需的時間」公式來計算需要的時間 [ t ] 。
    結果 = 10.95（2.7 個週期）。
    解釋：此次，最終目標不能降低到零，因此，我們採取目標可達到的範圍（7〜10）下限為之，即 7；
  3. 然後取該範圍的上限，即 10，為目標最早可達到的門檻，再计算结果。計算出的結果顯示
    1. 需要的時間在最早是 10.95 年
    2. 以及所需的改善期為至少 2.7 個週期
    因為每個品質改進週期與改善半衰期相同，就意味著最早將實現的目標是 2016 年（從 2004 年啟動值為 27 開始，並加上 3 個週期（2.7），即 12 年）。

自己嘗試一下

下面三個程式使用〝缺陷〞為例，改善前的數值高於改善後的數值。因此，計算半衰期與其他時間參數是正值。

然而，相反的也可以用﹝如：流程的遵從性從較低的層級到較高的百分比﹞。結果仍然可以計算，但將會呈現負值。

改善前與改善後的數值如果為 4.5%，可輸入 4.5﹝沒有百分比符號﹞或小數點，如 0.045。既然改善前要對照改善後的數值，請確認兩者都是用同樣的方式呈現，如 4.5% 降到 2.3% 或 0.045 降到 0.023。

時間的單位取決於使用者：如日、月、年；你輸入是哪一個，計算後答案將會是同類的時間單位。

Excel 電子表格
將數據放入B列的所有{數據}單元格;
對於每次計算，將其公式（從下面）放入三個{數據/公式}單元格中的單一相應單元格，
並將數據放入另外兩個{數據/公式}單元格
  A B C
1 Y {數據/公式} 指定時間段後「達到的改善目標」或「預期的結果」 [t-t0]
2 Y0 {數據} 在 t0的「當前的缺陷水平」
3 Ymin {數據} 最終目標」是可能的最大改進。為了減少缺陷，這一班將是零; 但是，有些流程的可實現目標無法是零。
4 ln(2) 0.69315  
5 t {數據/公式} 達到未來/期望目標 [Y] 所需的總時間。 [t-t0] 是在實施變更之前和之後實現改進所需的時間。
6 t0 {數據} 改進計劃的起點（通常在計算中設為零）
7 t½ {數據/公式} 當前半衰期（需要時間改進 50％）

① 計算改善半衰期 {B7}

利用改善前後的結果，並實現該結果所耗費的時間來取得「品質改善半衰期」。

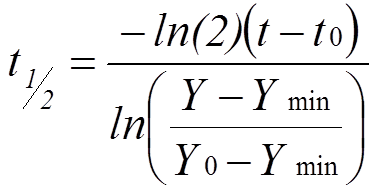
half-life equation

半衰期單位是與輸入的 [ t ] 相同；例如，如果 [ t ] 為「天」，那麼半衰期 [ t½ ] 也算成「天」。
在公式中使用 t0 = 0。

EXCEL:
t½ = -B4*(B5-B6)/LN((B1-B3)/(B2-B3))

 



② 預測未來的結果 {B1}

利用當前半衰期及可投入的時間來預設未來達成的目標。

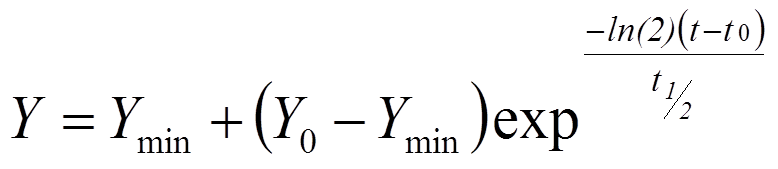
half-life equation
  • 〝最終的目標〞 [ Ymin ] 是最大可行的改善。
    對於許多減少缺陷的專案，這將是零；然而，一些作業具有不為零的改善目標，如在門診等待醫生的時間或每天處理的醫囑處方張數。
  • 達成的目標 [ Y ] 單位是與輸入的〝當前缺陷程度〞 [ Y0 ] 和〝最終的目標〞 [ Ymin ] 的單位相同。
  • 在公式中使用 t0 = 0。
EXCEL:
Y = B3+(B2-B3)*EXP(-B4*(B5-B6)/B7)

 



③ 預測改善所需的時間 {B5}

利用當前半衰期及可投入的時間來預設未來達成的目標。同時，轉換成多少半衰期的週期。

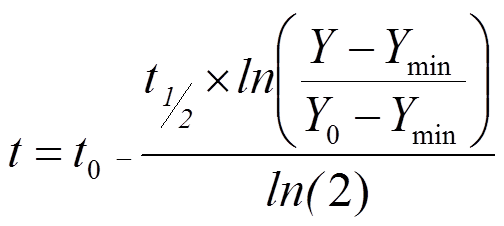
half-life equation

需要的時間 [ t ] 單位是與輸入的麼半衰期 [ t½ ] 相同；例如，如果 [ t ] 為「天」，那麼半衰期 [ t½ ] 也算成「天」。

在公式中使用 t0 = 0。

EXCEL:
t = B6-(B7*LN((B1-B3)/(B2-B3))/B4)

 



參考文獻：

  1. Anderson C. How Much Time Is Needed for Process Improvement?
    [www.bizmanualz.com]
  2. Schneiderman AM. Setting quality goals
    American Society for Quality Control, 1988; April: 51-7. (PDF:72KB)
    [www.schneiderman.com]
  3. Schneiderman AM. Origin of Schneiderman's Half-life Method
    [www.schneiderman.com]
  4. Schneiderman AM. Are There Limits to Total Quality Management?
    [www.schneiderman.com]