為何使用累積和管制圖?
一般普遍使用的管制圖有一個主要的缺點是他們僅使用流程收集到的資訊,且忽略整個時間序列的資料點所提供的資訊。Shewhart 類型管制圖沒有記憶:先前的觀察不影響未來失控旗標的概率。此外,它們對小變化不敏感。
累積和圖使用所有先前觀察值的未加權和。這個圖表有一個相當長的記憶。如果偏移1.5σ ~2σ 或更大,他們會非常有效。
另一個累積和管制圖受歡迎的理由是他們消除風險的能力。舉例來說,考慮意外事件通報系統不良事件需要即時受到管理。醫院不能直到資料點超過3個標準差外的管制界線才產生警示。反而,他們需要更敏感的偵測到微小的流程改變。
當必須確認介於平均值(1~1.5σ)微小改變,但僅可從流程管制取得極少的資料,累積和管制圖是一個非常好的解決方案。這應該考量應用於資料不頻繁且難以取得(不良事件),或費用高(滿意度調查),且想要偵測到流程操作中微小的改變。再者,他們對於樣本數 `n=1`,非常有效。
什麼是累積和管制圖?
就像管制圖,累積和管制圖常應用於時間序列的資料,是藉由畫出累計觀察值到目標值的差異所得到的。每個先前的資料點等同於累積和的值。
舉例來說,假設樣本數 ` n ≥ 1 ` ,且 ` bar x_j ` 代表第 `j` 個樣本的平均。接著,如果 `mu_0` 是流程平均值的目標,則累積和管制圖就能利用這些數值畫出來。
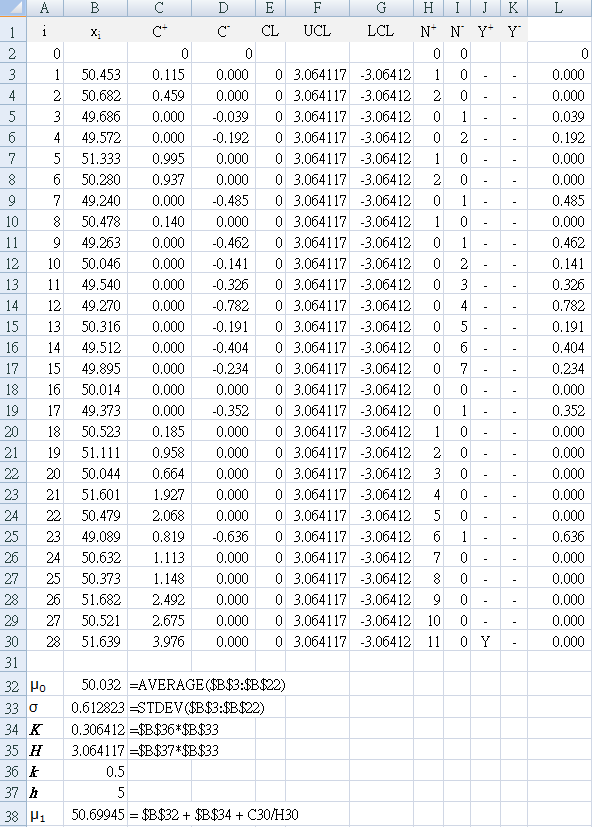
針對樣本 `i`,`C_i` 稱為直到第 `i` 個樣本的累積總和。累積和趨勢圖的分析純粹是視覺化的。不使用中位數也不用概率規則。如果流程位於目標值 `mu_0` 的管制中,累積和的資料點將圍繞著目標值維持水平。然而,如果平均值向上偏移 `mu_1 > mu_0`,則累積和 `C_i` 則會向上或正向偏移。相反的,如果平均值向下偏移 `mu_1 < mu_0`,則累積和 `C_i` 則會向下或負向偏移。 圖按方向的改變通常可利用流程改變進行解釋,且累積和統計值的資料點容易偵測到特定期間所發生的影響。因此,如果趨勢向上或向下,我們可以考慮流程平均值已經偏移,且應進一步探討可能的原因。
由於統計值是累計的,先前資料值所提供的資訊同樣被納入累積和圖中。在特殊原因被偵測到,且採取適當的反應,建議從 `0`「再開始」累積和的統計。否則,統計值持續指出特殊原因的狀況(當重新開始累積和圖時,另一種選擇是使用〝快速起始反應(FIR)〞,重新啟動累積和圖的統計從特定值開始,而不是0)
表列式累積和圖是如何創建的?
與傳統控制圖相比,表格累積和圖是獨特的,某些參數和統計信息必須在其創作中。
| 參數 | 描述 |
|---|---|
| `sigma` | ` sigma = sqrt((Sigma(x-bar x)^2)/(n-1)) ` |
| `mu_0` | 流程平均值(資料序列的平均)、參照值、或目標值。。 |
| `k` | 偵測平均值偏移一半的值。`k` 值從 `0.2` 到 `1.0`,但通常為 `0.5`,因為能配合傳統修華氏管制圖。 |
| `K` | `=k sigma`
在標準差的倍數中,流程平均值的偏移,為累積和管制圖想偵測到的。一般來說,介於 `0.5σ` 及 `1.5σ` 間。 |
| `h` | 決定決策間距 `H` 的決策參數。`h` 的值通常設定在 `4` (當 `k = 0.5`),可以配合傳統修華氏管制圖,但其他 `k` 及 `h` 的組合可用來符合其他管制圖的目標。 |
| `H` | `=h sigma`
`H` 為「決策間距」,主要用來運算管制界線。管制界線被設為 `hσ` 加上或減去目標(設為 `0`)。分析累積和管制圖,偵測特殊原因的唯一規則為超出管制界線。超出 `C_i^+` 或低於 `C_i^−i` 管制界線就是特殊原因的徵兆。 |
| ` C_i^+ ` | 高於目標值的累積總和,直到並包括第 `i` 個樣本。 |
| ` C_i^- ` | 低於目標值的累積總和,直到並包括第 i 個樣本。 |
| `FIR` |
`= (1/2)H`
快速最初回應或「先聲奪人」一般來說是 `H` 的一半,且在沒有資料時,為最初累積和管制圖的值。 |
` C_i^+ = max[0\, x_i - (T + k sigma) + C_(i-1)^+]`
` C_i^-``= min[0\, x_i - (T - k sigma) + C_(i-1)^-]`
或者,給出零以上的結果:
` C_i^-``= max[0\, (T - k sigma) - x_i + C_(i-1)^-]`
資料
(使用前 20 筆資料計算流程平均值及標準差)
50.453, 50.682, 49.686, 49.572, 51.333, 50.280, 49.240, 50.478, 49.263, 50.046,
49.540, 49.270, 50.316, 49.512, 49.895, 50.014, 49.373, 50.523, 51.111, 50.044,
51.601, 50.479, 49.089, 50.632, 50.373, 51.682, 50.521, 51.639
完成表 2 的步驟
B1 : "xi " (每個樣本的數值)
C1 : "`C_i^+` " (使用上述的公式計算累積和)
D1 : "`C_i^-` " (使用上述的公式計算累積和)
E1 : "CL " (中線)
F1 : "UCL " (管制上限)
G1 : "LCL " (管制下限)
H1 : "`N^+` " (零以上連續點的次數)
I1 : "`N^-` " (零以下連續點的次數)
J1 : "`Y^+` " (如果 `C_i^+` 超過 UCL,Y=yes )
K1 : "`Y^-` " (如果 `C_i^-` 低於 LCL,Y=yes )
A3 : "=A2+1"
向下拖動 A3 單元格(複製公式)直到 A30 為止 …
A30 : "=A29+1"
確認於 A2:A30,樣本的序列是從 0~28 號
對您的資料欄使用Excel命名範圍(例如,"$B$3:$B$30" 為 "myData")。
A33 : "`sigma`"
A34 : "K"
A35 : "H"
A36 : "k"
A37 : "h"
A38 : "`μ_1`"
B32 : "=AVERAGE($B$3:$B$22)"
B33 : "=STDEV($B$3:$B$22)"
B34 : "=$B$36*$B$33" (K = kσ)
B35 : "=$B$37*$B$33" (H = hσ)
B36 : "0.5"
B37 : "5"
D2 : "0"
D3 : "=MIN(0,B3-($B$32-$B$34)+D2)"
選擇 C3 及 D3 單元格,向下拖動(複製公式)直到 D30 為止 …
C30 : "=MAX(0,B30-($B$32+$B$34)+C29)"
D30 : "=MIN(0,B30-($B$32-$B$34)+D29)"
欄 L 使用 `C_i^-` 的第二個公式來確認欄 D 中的結果。
` C_i^-``= max[0\, (T - k sigma) - x_i + C_(i-1)^-]`
L3: "=MAX(0,($B$32-$B$34)-B3+L2)"
F3:F30 : "=$B$35" (`H = h sigma` 其中 `h=5`)
G3:G30 : "=-$B$35" (左側有減號)
K3 : "=IF(D3<=G3,"Y","-")"
選擇 J3 及 K3 單元格,向下拖動(複製公式)直到 K30 為止 …
J30 : "=IF(C30>=F30,"Y","-")"
K30 : "=IF(D30<=G30,"Y","-")"
確認 J30 的結果為 Y
I2 : "0" (設定 `N_0^+` 始於0)
H3 : "=IF(C3>0,H2+1,0)"
I3 : "=IF(D3<0,I2+1,0)"
選擇 H3 及 I3 單元格,向下拖動(複製公式)直到 I30 為止
H30 : "=IF(C30>0,H29+1,0)"
I30 : "=IF(D30<0,I29+1,0)"
確認你 J30 的結果顯示 "Y", `N_28^+ = 11`。
`mu_1 = mu_0 + K + (C_i^+ \/ N_i^+)`
其中 `C_i^+` 是 `C_i^+` 的值超出控制限制時。當管制限制被超過時,`N_i^+` 為連續大於零的次數。在這個例子中,`N_28^+ = 11` 和 `C_28^+ = 3.976`。 改變的過程均值 `mu_1`(或 `bar x_1`)
= 50.699
`mu_1 = mu_0 - K - (C_i^+ \/ N_i^+)`
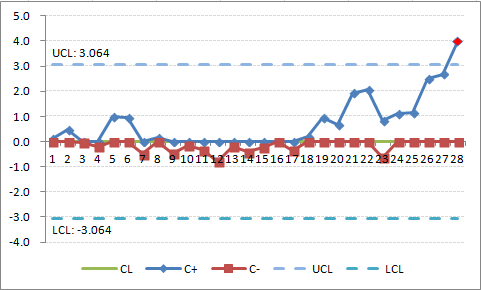
一旦流程已經被校正回到目標, `C_i^+` 及 `C_i^-` 的值應該被設定為 0。然而,有一個方稱為快速起始反應(Fast Initial Response, FIR),利用它,值不用設回 0,但會被設為一個特定值,通常是 2 倍的標準差。這提供一個快速回應到偏離目標的作業。你也可以利用FIR開始畫累積和圖。圖 4 顯示當使用FIR的方法時,圖 3 使用 2 個標準差而不是 0。意即,表 2,會有以下改變:
D2 : "=-2*$B$33" (左側有減號)
你可以看到圖 2 `C_i^+` 及 `C_i^-` 距離 0 更遠。如果流程偏離目標,累積和管制圖將能較快偵測到。如果在管制中,累積和值的趨勢將回到 0,如第 7 個資料點。

The tabular cusum used in the basic example above has a single measurement in each sample (subgroups n = 1). Cusum can also be used for the averages of rational subgroups (n > 1), for example, the averages of likert scores on a satisfaction survey each day at an outpatient clinic. In this case, replace σ by `σ_x = σ ÷ sqrt(n)`. With Shewhart charts, the use of averages of rational subgroups substantially improves control chart performance.
However, this does not always happen with the cusum. If, for example, you have a choice of taking a sample of size n = 1 every half-hour or a rational subgroup sample of size n = 5 every 2.5 hours (note that both choices have the same sampling intensity), the cusum will often work best with the choice of n = 1 every half-hour. Only if there is some significant economy of scale or some other valid reason for taking samples of size greater than one should subgroups of size greater than one be used with the cusum.
Example: Satisfaction survey
This section uses satisfaction surveys as the example, based on a 5-point Likert scale for answering a question about the effects of a quality improvement strategy.
The scenario was an outpatient clinic for a single doctor. The quality improvement team were using PDSA methodology, and wanted to test the effectiveness of a strategy that they designed to resolve a problem that patients complained of in the free-text section of satisfaction questionnaires.
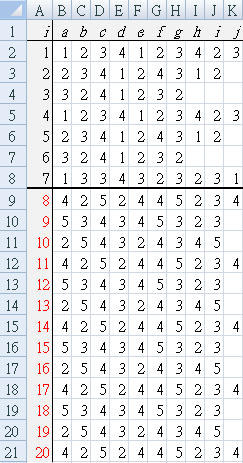
Each patient, as they left the clinic after seeing the doctor, was asked to rate the result using a 5-point Likert scale (1=very unhappy, 5 extremely satisfied). Table a1 shows the Likert score given by each patient (a~j). Rows indicate "day at clinic", for example, all the survey results for day 1 are in B2 to K2 {1, 2, 3, 4, 1, 2, 3, 4, 2, 3}.
Baseline data for one week (7 days), shown by a thick black line between day 7 and day 8.
From day 8, the new method was continued for another two weeks.
The result of interest was improvement, so a one-sided CUSUM `C^+` was used. Data was analysed in the following ways:
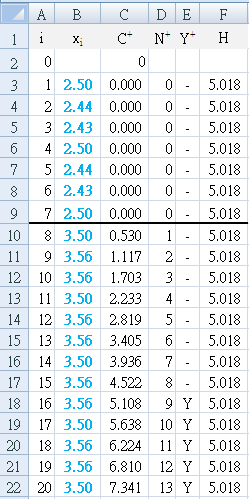
- Each day, the average satisfaction was calculated and used as a single data value (n=1) to calculate (Table a2) and graph (Figure A2) the result.
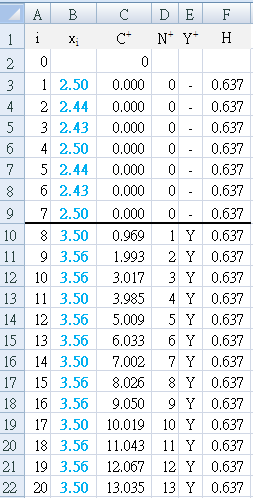
- Each day, the average satisfaction was calculated and used as a single data set (n>1) containing multiple values (different number of patients each day). The calculations were adjusted to reflect this (Table a3) and graph (Figure A3) by replacing σ with `sigma_x = sigma ÷ sqrt(n)` (Figure A1a)
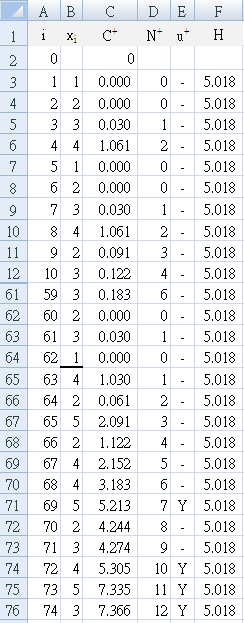
- Each patient value (n=1) was used to calculate the CUSUM values (Table a4) and graph (Figrue A4). There were 62 patient surveys collecting during the baseline period.
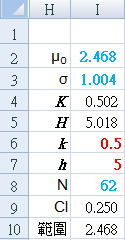
Set CUSUM parameters manually:
k and h
{red numbers}
Calculated from raw data {blue numbers}:
I2: "=AVERAGE($B$3:$K$9)"
I3: "=STDEV($B$3:$K$9)"
I8: "=COUNT($B$3:$K$9)"
Derived CUSUM calculations:
I4: "=$I$6*$I$3"
I5: "=$I$7*$I$3"
I9: "=CONFIDENCE(0.05,$I$3,$I$8)"
J10: "=CONCATENATE(TEXT($I$2-$I$9,"0.000"),"~",TEXT($I$2+$I$9,"0.000"))"
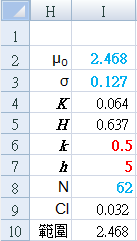
I3: "=STDEV($B$3:$K$9)/SQRT($I$8)"
Results
All three methods show that the baseline system was breached starting from day 8, however, they differed in how early the change was detected.
Using the Excel function to calculate 95% confidence interval, the average satisfaction during the two periods was:
Baseline: 2.468 (2.218 ~ 2.718)
After strategy: 3.536 (3.468 ~ 3.603)
By looking at the core calculation area, we can see that the CUSUM has detected an increase (change)
-
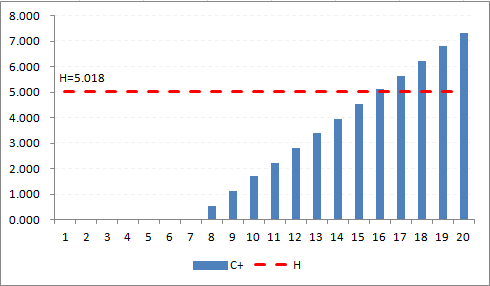
Table a2 first detects the change (`Y^+`= "Y") at E18, which is day 16, 9 days after the improvement strategy was begun. Using `N^+` to backtrack, we can see that the change started (`N^+` = "1") on day 8.
The result is easily seen in Figure A2, where the first positive bar column appears at day 8, and the decision interval (H=5.018) is breached at day 16. -
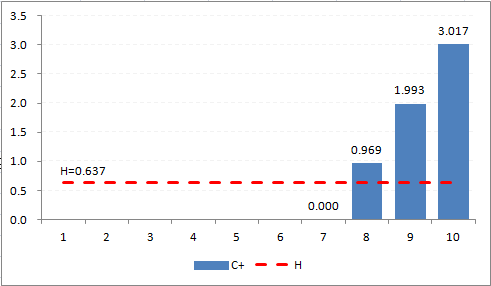
Table a3 first detects the change (`Y^+`= "Y") at E10, which is day 8, 1 day after the improvement strategy was begun.
The result is seen in Figure A3, where the first positive bar column appears at day 8, and immediately breaches the decision interval (H=0.637). -
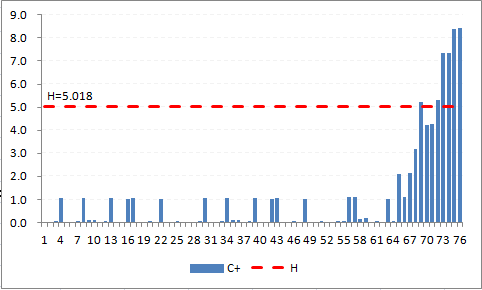
Table a4 first detects the change (`Y^+`= "Y") at E71, which is patient 69, the fifth patient on day 8, the day that the improvement strategy was begun.
The result is easily seen in Figure A4, where the consistently positive bar columns appear at patient 63, and reaches the decision interval (H=5.018) by patient 69.
關鍵文獻
-
Provost LP, Murray SK.
The health care data guide. Learning from data for improvement.
(2011)
John Wiley & Sons Inc, San Francisco.
[ www.josseybass.com/go/provost] -
Morton AP, Whitby M, McLaws ML, Dobson A, McElwain S, Looke D, Stackelroth J.
The application of statistical process control charts to the detection and monitoring of hospital-acquired infections.
J. Qual. Clin. Practice. 2001; 21: 112-117.
[ https://www.ncbi.nlm.nih.gov/pubmed/]