院內感染(HAI)
當使用每月的感染資料,Shewhart、CUSUM 及 EWMA 管制圖能用於沒有分母資料,在感染管制計畫中,這部份的資料常難以定義,且長花很多時間收集。 這可用於不良事件比率不超過10%。
感染率的變化可以突然大量增加或持續上升來表示。 因為 Shewhart 管制圖更好地檢測前者,而 CUSUM 和 EWMA 圖後者,最好一起使用這兩種。
CUSUM 觀察圖
CUSUM 統計檢定
視覺解釋
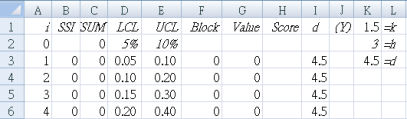
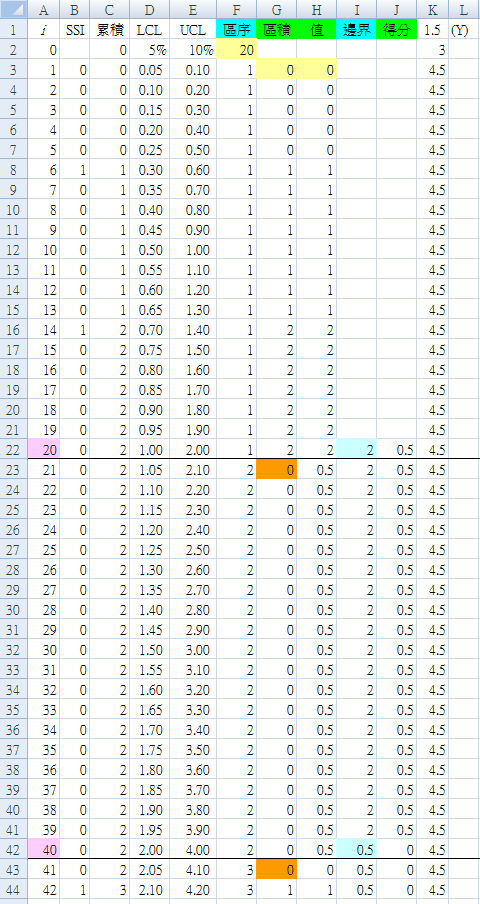
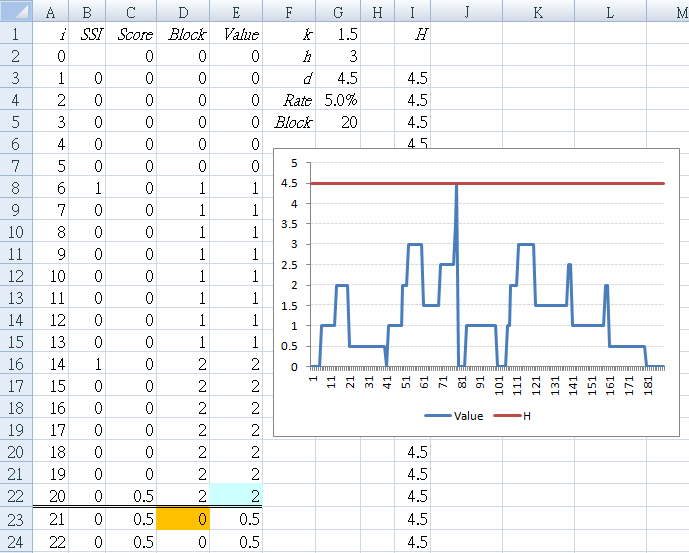
標駐區塊的疆界。在 A 欄,每 20 個 ($F$2) 手術,以粉紅色的背景標駐區塊的終點;也就是 i = 20, 40, 60, 80, 100, 120, 140, 160, 180 在 A22, A42, A62, A82, A102, A122, A142, A162, A182。
表 4 在每個區塊的最後增加一條黑線,讓區塊的範圍更清楚。
請注意,接著在每個區塊 CUSUM 的第一個值將重置為零。在 G 欄,每 20 件 ($F$2) 手術後,在每個區塊的開始設定橘色的背景;也就是,i = 21, 41, 61, 81, 101, 121, 141, 161, 181 在 G23, G43, G63, G83, G103, G123, G143, G163, G183。
將每個區塊最後一個 CUSUM 值背景改為藍色。也就是在 I 欄 i = 20, 40, 60, 80, 100, 120, 140, 160, 180 在 I22, I42, I62, I82, I102, I122, I142, I162, I182。
I 欄的 CUSUM 值隨區塊而變化,並確保獨取前一個區塊的最後一個值(就是我們剛剛標註藍色背景的部份)。
快速模板
如果你利用上述的方法一步步完成實例,你已經了解基本方法,接著使用以下版本使後續的例子更能利用
B1 : "SSI"
C1 : "Score"
D1 : "Block"
E1 : "Value"
| F1 : "k" | G1 : "1.5" |
| F2 : "h" | G2 : "3" |
| F3 : "d" | G3 : "=G1+G2" |
| F4 : "Rate" | G4 : "0.05" |
| F5 : "Block" | G5 : "=1/G4" |
D2 : "0"
E2 : "0"
D3 : "=IF(MOD(A3,$G$5)=1,0,(B3+D2))"
E3 : "=IF(A3<=$G$5,(B3+E2),IF(E2>=$G$3,0,(D3+C2)))"
採用此方法於某一家醫院
外科手術 #1
從 2001 年 12 月 ~ 2016 年 08 月,867 件手術,有 40 件感染,感染率為 4.6%。有感染的手術序號列於下方:
9, 11, 19, 24, 30, 48, 58, 74, 80, 110,
113, 130, 135, 151, 186, 189, 228, 239, 273, 293,
319, 337, 339, 380, 384, 437, 458, 480, 482, 484,
523, 529, 553, 611, 702, 733, 750, 793, 809, 810
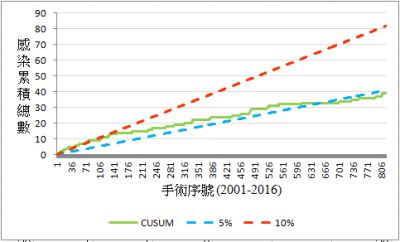
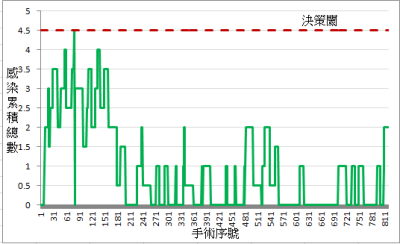
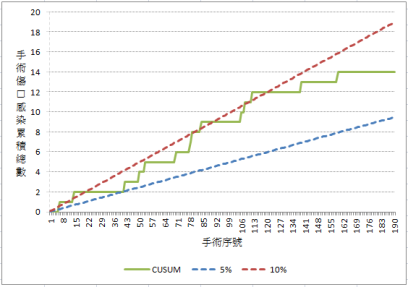
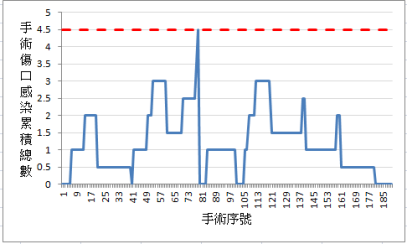
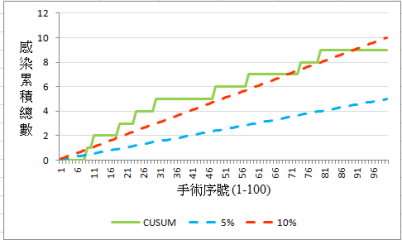
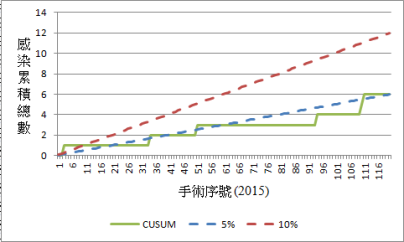
解釋: 在初期(前 100 個手術),感染件數的 CUSUM 值大多在或超過 10% 管制上限(圖 6)。 且閾值在第 80 筆手術被超過了(圖 7)。此後,SSI 件數變得更水平 ,接著,在最近一年,傾向管制下限,低於 5%。為了進一步探討這兩個期間,資料分為兩個時期:圖 8 (前 100 筆手術)及圖 9 (最近一年)。這些圖形證明 SSI 比率在該手術有明顯的改善(降低)。
實踐事例
對每個事例:
- 畫出 CUSUM 觀察圖
- 畫出 CUSUM 統計檢定圖
- 解釋結果
外科手術 #2
從 2000 年 10 月 ~ 2016 年 08 月,771 件手術,有 57 件感染,感染率為 7.4%。有感染的手術序號列於下方:
21, 27, 43, 45, 46, 48, 49, 51, 52, 58,
69, 80, 82, 87, 90, 95, 96, 98, 100, 101,
106, 113, 119, 120, 125, 137, 140, 161, 164, 170,
173, 185, 209, 215, 224, 243, 257, 273, 285, 298,
307, 310, 313, 318, 331, 337, 360, 373, 403, 440,
638, 658, 687, 705, 715, 716, 743
外科手術 #3
從 2001 年 12 月 ~ 2016 年 02 月,469 件手術,有 20 件感染,感染率為 4.3%。有感染的手術序號列於下方:
30, 33, 42, 43, 45, 46, 58, 139, 235, 255,
274, 321, 324, 340, 401, 404, 420, 436, 446, 465
病人滿意度
資料
82, 79, 84, 82, 92, 80, 94, 78, 83, 84, 92, 84,
89, 88, 93, 84, 98, 92, 87, 94, 93, 95, 91, 84,
95, 92, 95
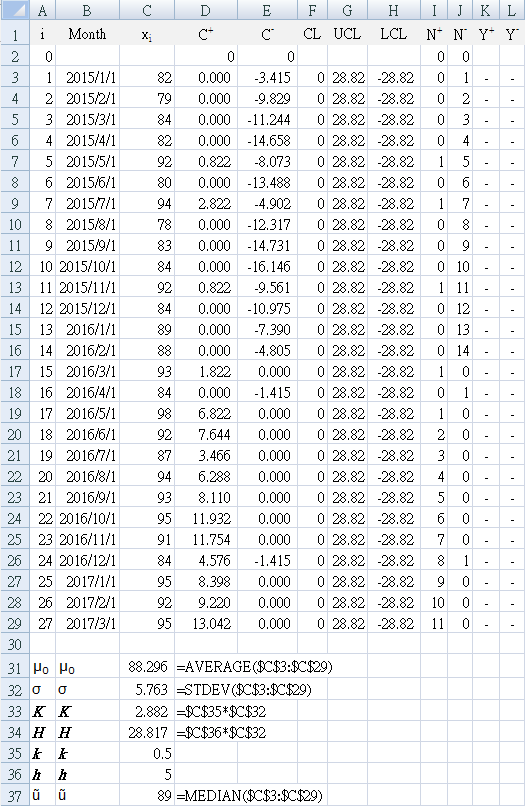
資料是每月病人滿意度,表示為雙頂指標(在Likert量表 1分-5分上給出 4分 或 5分 的人數量)導出的百分比。 在圖10中,使用中心線的中值89%來顯示每月滿意度作為推移圖(趨勢線)。 推移圖表顯示沒有違反任何非隨機變化規則可暗示改進。
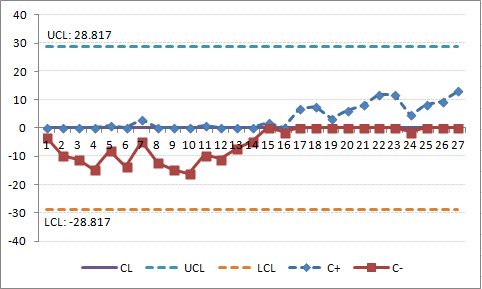
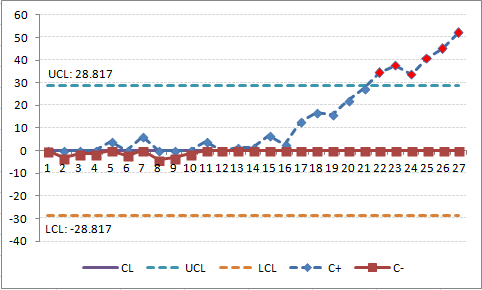
圖 11是表 5 中的數據的CUSUM,使用系統平均值(88.296)作為目標(目標)。 這示出了在圍繞 i = 16 的過程變化的引入之後,從目標(零中心線)開始的逐漸的持續變化,儘管前幾個月具有差的性能(在中心線之下)。 這在 CUSUM 圖表中比推移圖表(其中沒有違反任一隨機變化規則)在視覺上更明顯。
圖12 是相同資料的 CUSUM,但是使用 85%為目標。 (要在 Excel工作表中查看此效果,請將單元格C31更改為“85”) CUSUM 圖表最初顯示為平坦的斜率,表明性能接近目標。斜率在 i = 11處開始上升(保持在中心線上方)並且在 i = 22 處穿過 H 閾值(UCL),指示 月度業績大於85%的目標。 過程斜率繼續上升,表明目標(最後6個資料點)之上的持續性能。
繼續使用目標為 85%的工作表,並將 `C_i ^ +` 重置為 `2sigma` 的FIR;
C23: "=2*$C$32"
你是否發現,CUSUM 線繼續上升,並且在四個資料點之後再次達到上限控制限。
風險分層
圖13顯示了在某醫院在一年內闌尾切口傷口感染(SSI)的 CUSUM 圖。圖 13(a) 是當年整體手術的 CUSUM 圖加上醫院訂定的目標:下限為1.5% 和上限為 3.25%。圖 13(b) 是相同的醫院資料,但具有從同一時期的 NHSN 資料庫添加的對等組統計。圖 13(c) 按 NHSN 風險(0 級、1級)和 圖 13(d) 分層,NHSN 風險(2 級、3 級)分層。虛線表示 NHSN 對等體組級別。
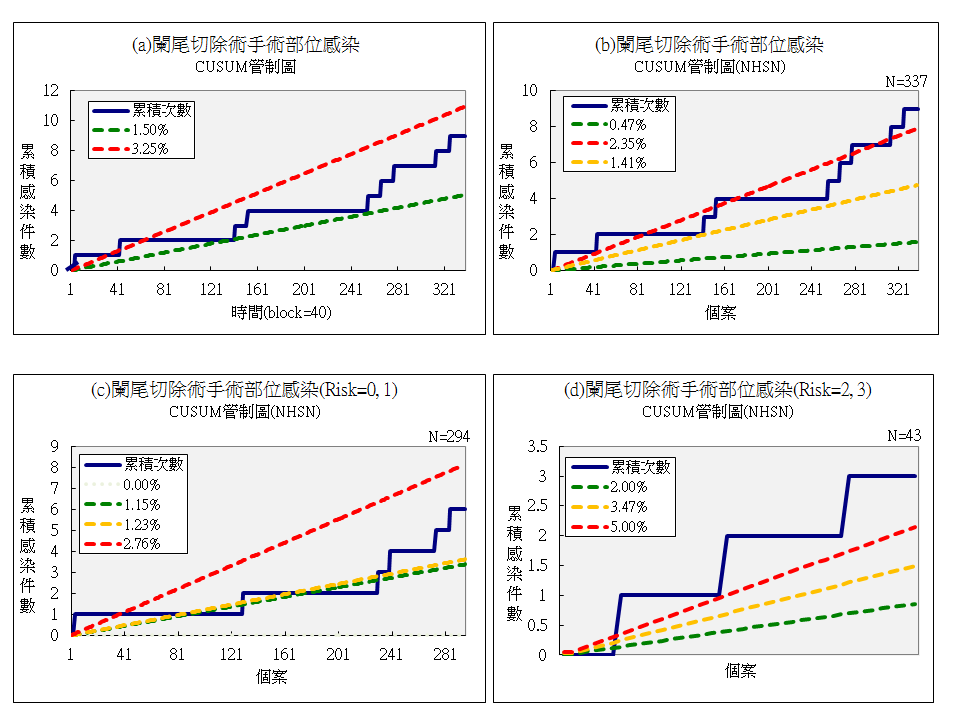
解讀:儘管醫院在時間過程中已經達到了其自己的目標(13a),但是通過與NHSN對等組(13b)相比,它在圖的右三分之一處的上限(虛線紅線)上方徘徊,並繼續惡化,直到結果高於 2.45% 的上限。然而,風險分層表明這種影響不存在於風險類別 0級 和 1級(13c),但風險類別 2級和 3級(13d)在整年中真的很糟糕,遠高於該組的5%上限。這是品質改進需要關注的分組。
技術考核
累積和失效分析可有效監測健康照護程序執行的表現。 最困難的地方是決定什麼是可接受和不可接受的故障率。 結果以兩種類型的圖形顯示:
- 累積失敗次數的垂直軸(y)對應嘗試次數的水平軸(x)。 因此,零失敗率只能畫出水平線,但 100% 失敗率畫出的是通過軸的 45 度線。 由於累積和失敗率永遠不會下降,因此圖形只會上升,但確實提供了簡單直觀資訊有關程序粗酪成功率或失敗率的定義計數。 (範例請參閱HAI 的部分)
- 累積和的值繪製在 y 軸上的累積值與 x 軸上的嘗試次數。 在可接受的表現水平下,累積和曲線平坦或向下傾斜,而在不可接受的表現水平下,曲線向上傾斜並最終穿過決策區間。
繪製累積和管制圖是長期表現監控的理想選擇(如在持續專業發展中),因為很容易在一段可接受或不可接受的表現之後,很容易識別表現的變化。 這在累積失效圖上要視別困難得多。
然而,累積失效圖用於監控受訓者, 通常,通過在同一計算中添加具有更高級的類型1錯誤“警報”行, 以提醒培訓師受訓者正在接近不可接受的表現。
表現的測量以二元結果(程序的成功與失敗)來呈現,1 表示失敗。 在開始監測之前,必須明確說明什麼是“可接受的”和什麼是“不可接受的”。 理想情況下,這些基於權威醫學專業機構發佈的應該是普遍接受的標準。 不幸的是,這種績效標準很少見,或者正在制定過程中。 在此之前,參與監測的專家應首先決定標準。
CUSUM監測在使用該測試的地方,參與的醫生認為該技術是可以接受的,特別是當作個人自我評估工具。 但是,他們認可其作為基礎認證的接受性不太高。
儘管SPC的使用在某些學科中已經確立,例如實驗醫學科,但其在臨床照護過程中的應用構成特殊的挑戰。 Shewart 管制圖被設計用在在大批量製造過程中檢測過程均值中較大但瞬態的變化。 這限制了它們在臨床照護過程中的應用,原因有兩個。
- 首先,臨床過程的輸送量通常非常慢; 例如:外科醫生一天可能執行不超過一到五次手術。 性能監測系統要求在分析之前累積大於1的樣本量既沒有必要又不方便。
- 其次,對於臨床照護,該程序的平均值即使微小變化也值得關注; 例如:死亡率、併發症發生率或手術失敗率的不良惡化。 臨床監測要求在發生太多不良結果之前就要對不良性能進行早期預警。
CUSUM圖表是客觀的,且具有很大的視覺吸引力。 對於受訓者來說,它從圖形上顯示了學習曲線以及個人如何隨著時間的推移和更多的練習取得進步。 這可以輔助當前依賴外部觀察員檢查的制度, 當然比在假定具備能力之前依靠執行大量的程序要好的多。 醫生確實有個別不同的學習曲線。
型一錯誤:誣告的機率α、偽陽性(為統計學中推論統計學統計術語)。就法庭示例而言,型一錯誤對應於對無辜被告定罪。
型二錯誤:虛假證明的機率β、偽陰性(為統計學中推論統計學統計術語)。就法庭示例而言,型二錯誤對應於無罪釋放罪犯
據說CUSUM圖在以下情況下發出信號 `C_n` 跨越預定的決策區間, `H`.`H_0` 表示每個可接受的決策級別之間的值。 這些間隔可以在 CUSUM 圖上標記為水平線。 當一條線穿越時, `C_n` 傳統上恢復為零,但如果重複的決策間隔以圖形方式堆疊,則可以構建學習曲線。
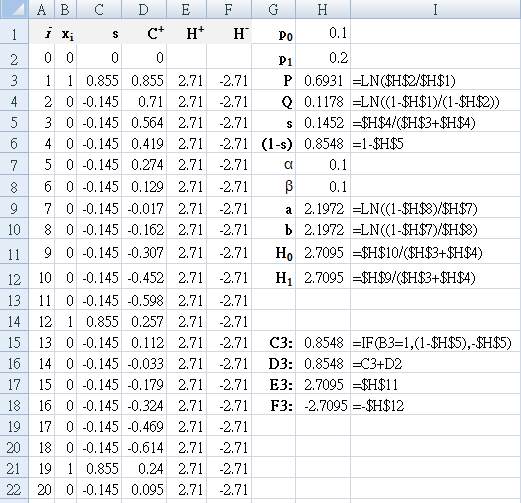
常用值:可接受的故障率 `p_0` = 0.1 (10%),
不可接受的故障率
`p_1` = 0.2 (20%), `α` = 0.1, `β` = 0.1
`P = ln(p_1 \/ p_0)\, Q=ln((1 - p_0) \/ (1-p_1)) `
程序 `s` 的成功是根據這兩個比率計算的,失敗也是如此
`(1-s)`.
`p_0 = 0.1\, p_1 = 0.2\, s = 0.15\, (1-s) = 0.85`
`a = ln((1 - β) \/ α)`
`b = ln((1 - α) \/ β)`
`H_0 = b \/ (P+Q) = 2.71`
`H_1 = a \/ (P+Q) = 2.71`
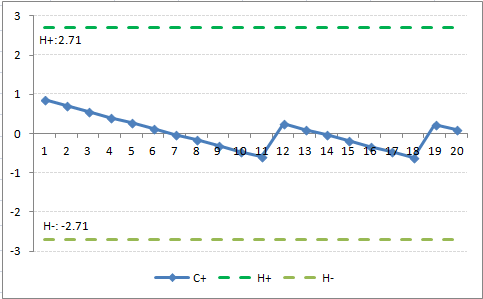
CUSUM 間隔管制圖
利用CUSUM的方法進行更嚴密的監控,更重視保持流程在特定的目標,而不是讓其靠近管制界線 由於更嚴密的監管,超出管制的訊號將不常指出流程產生不合格的產品;超出管制的訊號則是代表應採取管制行動以預防產生不合格的產品。 由於CUSUM的方法是早期指出流程的變化,他們與管理哲學一致,鼓勵第一時刻就把事件作對。 CUSUM的使用也符合異常管理理論,因為CUSUM指出例外管理的領域。
Lucas (1985) 確定 Poisson CUSUM 每個抽樣間隔的數量 (g-chart) 及事件間時間間隔 (t-chart)。 g-chart 可被用來計算不好單位(如:手術傷口感染)間好單位的數量(如:手術)。 除了設計教案,可能的應用包括監測意外事件間的時間、文書工作發生一個或多個錯誤、或先天異常的發生率。 〝數量〞這個詞較〝不良品〞(不遵從、不遵從)受喜愛,因為〝數量〞的應用層面較廣。 對 g-charts,期望缺陷間的時間(或連續不好的單位間好單位的數量)越大越好。 T-chart 對於偵測事件間時間的變化是很有用的,且訊號指出是否好單位的數量降低,壞單位的發生率(缺陷、感染)增加。
錯誤率可以測量為“每{監視的單位數}的缺陷” (例如,每百萬單位錯誤數)及“每{監視的機會數量}的缺陷”(例如,每百萬機會錯誤數)。 以手術預防性抗生素為例,每個手術有幾個步驟,包含抗生素的選擇、劑量、給藥時間(有三個部份:術前、術中、術後中止)。總共監測五個項目(忽略討論其他牽涉到病人及藥物辨識的步驟)。 如果全部遵從指引,病人被紀錄為〝正確〞治療;如果任一項目未遵從(如:術前抗生素太早給、術後抗生素未停用),病人則被記為〝未正確〞(缺陷、不符合)。 亦即,每個病人被視為一個單位,並評為〝是〞(完全遵從)或〝否〞。 這就是〝單位錯誤率〞指標,分母為使用手術預防性抗生素的病人數。 分開來看,手術的每個步驟都被監測,所以每個病人有五個機會未遵從指引。
這是〝機會錯誤率〞指標,其中分母是給予外科抗生素預防性治療的患者人數乘以所涉及的步驟數。, 分母為使用手術預防性抗生素的病人數乘以步驟數。 兩項指標都是很重要的,且能利用 t-型圖 CUSUM 及 g-型圖管制圖進行監測。
CUSUM 控制方案通常通過計算其平均遊程長度(ARL)來評估。 ARL 是在顯示失控之前採集的平均樣本數。 當過程處於其目標水準時, ARL 應該較大,而當過程轉換到不期望的水準時,ARL 應該較短。 在很多指標,單位錯誤率管制內的 ARL被設定為 100;對機會錯誤率管制內的 ARL 被設定為 1000。 機會錯誤率管制內的 ARL 設定大於單位錯誤率管制內的 ARL,為了避免流程出現管制外的訊號(亦即避免虛驚)。
記數資料 CUSUM 的設計
- 使用可接受的比率 `u_a`,選擇參考值k,且平均計數資料 `u_d` 能快速被偵測到。
雖然,`u_a` 的期望值(或目標)常是 0,但 0 通常無法使用於設計公式。實務上,`u_a` 常被選為靠近目前平均值;這代表目前系統的表現。 參考值應被選為接近:兩個不好的事件間,好事件的件數 CUSUM g-chart {POISSON}
惡化方向 `k_p = (μ_d - μ_a)/(ln(μ_d) - ln(μ_a))`事件間的時間間隔 CUSUM t-chart {TBE}
`k_b = (ln(μ_d) - ln(μ_a))/(μ_d - μ_a)` - 從 Lucas (1985) 表中選擇決策間隔值 `h`,主要是由期待管制中的 ARL 所決定的;也就是說,錯誤的超出管制界線的訊號(偽陽性)是可接受的次數。 透過使用 ARL 表在FIR CUSUM,可避免剛開始超出管制界線的狀況。Lucas (1985) 相關表如下(〝惡化方向〞意味著方向的改變表示缺陷的增加/品質的降低)。
表 7、決策區間的劉易斯查找表 惡化方向 g-型圖
{POISSON}t-型圖
{TBE}增加 表3 表10 減少 表5 表 - 對於事件間時間間隔 CUSUM (t-chart),`h` 是利用常態參考值ARL 表得來的 `k_t=k_b × μ_a`,或也許從 `μ_d × μ_a` 所得到的。 由於事件間間隔時間是連續性的資料,在表中插值也許是需要的。ARL 插值使用對數內插值(線性內插值是用自然對數(ARL)),介於兩個最接近的常數 `k` 間(以恆定比例 `h / k`)。
`k_t = ( ln(μ_d ÷ μ_a )) / ((μ_d ÷ μ_a) - 1 )`
從表中取得的 `h_t` 值被歸一化以獲得由具有 `h_b =(h_t × &mu; _a)` 的控制方案使用的判定間隔值(`h_b`)。`x = x_2^f × x_1^(1-f)` (Deserno M)
從表中取得的 `h_t` 值被歸一化以獲得由具有 `h_b =(h_t × &mu; _a)` 的控制方案使用的判定間隔值(`h_b`)。 - 使用上述的 `C_i^+` 和 `C_i^-` 方程來計算。
簡化 ARL 計算
`ARL = (exp(-2Δb) + 2Δ -1) / (2 Δ^2)` (Siegmund's approximation, Montgomery p.323)
for `Δ \ne 0` (if `Δ=0` use `ARL = b^2`)
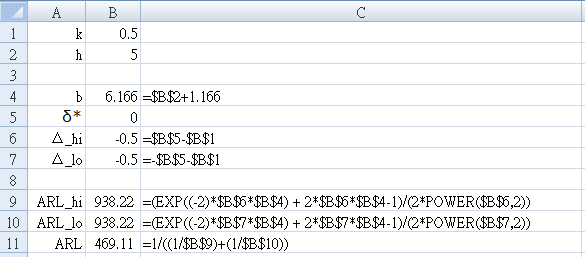
- 開始新的工作表來測試一個雙面的 cusum,使用 `k=1 / 2, h=5`.
- 在A欄中輸入參數名稱,如圖 15 所示。
- 設置 `k=1 \/ 2` → B1 = 0.5
- 設置 `h=5` → B2 = 5
- 將欄C中顯示的方程輸入單元格中緊接其左側的欄B中
- 對於穩定狀態(沒有從平均值的移位,即 `δ^* = 0`)
設置 `δ^* = 0` → B5 = 0 - 確保您的結果是 `ARL = 469.1`
示例:事件之間雙向CUSUM間隔管制圖
對意外事件的資料,每一個新發生的事件很值得以 CUSUM 進行更新。
以比率/月為基礎設計 CUSUM,接著再轉換為每日為基礎進行。
(Table 15 in Lucas JM. Counted data CUSUM's. Technometrics. 1985; 27(2): 129-144)
- 將資料匯入 Excel 的工作表。確認資料被轉換為日期型態。
- 旁邊的欄位計算每一個事件到前一個事件間的日數。
- 使用前五年的資料計算平均意外事件的水準 `u_a`
- 設定被監測的流程水準為 `δ^* = 1`, ,且利用它來計算雙向趨勢(增加、減少)率 `u_d`
- 計算雙尾: `k_b = (ln(u_d) - ln(u_a) / (u_d - u_a)`
- 使用30作為每月的天數,且重新計算 `k_b` 天數
`k_b = k_b × 30` - 使用 Lucas 表,找到適當的 `h_t`,(使用FIR特性)
- 為了執行,使用
`h_b = h_t \/ u_a` and `S_0 = h_b \/ 2` - 使用上述所討論的等式,計算每邊的 CUSUM 值
`S_i = max(0\, k_b - Y_i + S_(i-1))`
解決方案:事件之間雙向CUSUM間隔管制圖
| 參數 | 增加 | 減少 |
|---|---|---|
| `u_d` | 3.0 | 1.0 |
| `k_b` | 0.41 | 0.69 |
| `k_b` (days) | 12.3 | 20.7 |
| `h_t` | 5.6 適合兩者 | |
對於實現,使用 `h_b = h_t / u_a = 5.6 / 2 = 2.8` 個月,或者 84天,使用 `S_0 = 42` 天.
實現CUSUM以檢測速率的增加使用
`S_i = max(0\, 12 - Y_i + S_(i-1))`
在前五年的資料中沒有給出信號,並且沒有(假)檢測到第二個五年的資料增加。
實現 CUSUM 以檢測速率的降低使用
`S_i = max(0\, 12 - y_i + S_(i-1))`
在前五年中不給出假信號,並且給出指示使用數據點 128-130 的平均值減小的第一信號。 如果使用FIR特徵重新啟動 CUSUM,則在四次觀察之後,CUSUM 將再次發出信號。
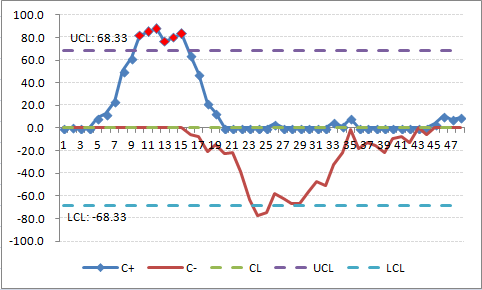
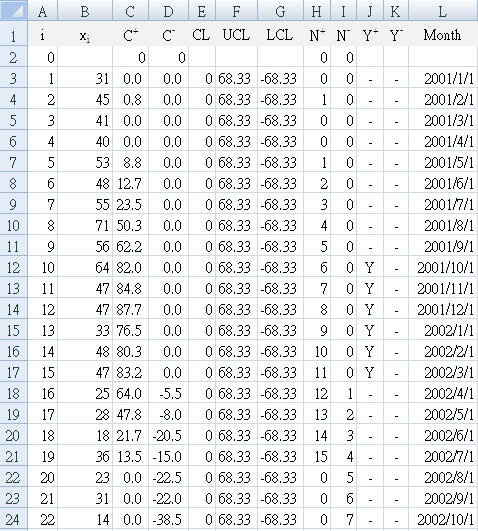
以 HIV/AIDS 為例進行自我測試
實現以下數據的 CUSUM 圖表,並解釋您的發現。 資料來源:表1 於 [Adeoti OA]
| 月 | 2001 | 2002 | 2003 | 2004 |
|---|---|---|---|---|
| 01 | 31 | 33 | 33 | 36 |
| 02 | 45 | 48 | 48 | 28 |
| 03 | 41 | 47 | 26 | 24 |
| 04 | 40 | 25 | 26 | 43 |
| 05 | 53 | 28 | 30 | 32 |
| 06 | 48 | 18 | 41 | 26 |
| 07 | 55 | 36 | 40 | 44 |
| 08 | 71 | 23 | 27 | 25 |
| 09 | 56 | 31 | 49 | 48 |
| 10 | 64 | 14 | 41 | 51 |
| 11 | 47 | 6 | 51 | 41 |
| 12 | 47 | 16 | 13 | 46 |
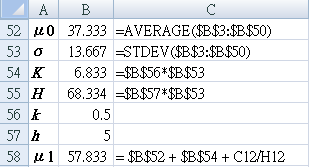
D3:"=MIN(0,B3-($B$52-$B$54)+D2)"
E3:"0"
F3:"=$B$55"
G3:"=-$B$55" (前減號)
H3:"=IF(C3>0,H2+1,0)"
I3:"=IF(D3<0,I2+1,0)"
J3:"=IF(C3>=F3,"Y","-")"
K3:"=IF(D3<=G3,"Y","-")"
關鍵文獻
- Montgomery DC. Introduction to statistical quality control. 3rded. John Wiley & Sons Inc. 1997
- Provost LP, Murray SK. The health care data guide. Learning from data for improvement. John Wiley & Sons Inc, San Francisco. 2011
- Morton AP, Whitby M, McLaws ML, Dobson A, McElwain S, Looke D, Stackelroth J. The application of statistical process control charts to the detection and monitoring of hospital-acquired infections. J. Qual. Clin. Practice. 2001; 21: 112-117.
風險分層
-
Coory M, Duckett S, Sketcher-Baker K.
Using control charts to monitor quality of hospital care with administrative data.
Int J Qual Health Care. 2008; 20(1): 31-39.
[
www.ncbi.nlm.nih.gov/pubmed]
Uses risk-adjusted, expected-minus-observed CUSUM control charts for 30-day, in-hospital mortality rate following admission for acute myocardial infarction. -
Noyez L.
Control charts, Cusum techniques and funnel plots. A review of methods for monitoring performance in healthcare.
Interact CardioVasc Thorac Surg. 2009; 9(3): 494-499.
[
doi: 10.1510/icvts.2009.204768]
Includes a discussion of CUSUM charts including cumulative failure chart, standard non-risk-adjusted CUSUM chart, risk-adjusted CUSUM chart, and funnel plots, especially in cardiac surgery.
技術考核
-
Lim TO, Soraya A, Ding LM, Morad Z.
Assessing doctors’ competence: application of CUSUM technique in monitoring doctors’ performance
- Starkle T, Drake EJ. Assessment of procedural skills training and performance in anesthesia using cumulative sum analysis (cusum). Can J Anaesth. 2013; 60 (12): 1228-39.
- Campbell RD, Hecker KG, Biau DJ, Pang DSJ. Student Attainment of Proficiency in a Clinical Skill: The Assessment of Individual Learning Curves PLoS One. 2014; 9(2): e88526.
- Naik VN, Devito I, Halpern SH. Cusum analysis is a useful tool to assess resident proficiency at insertion of labour epidurals. Canadian Journal of Anesthesia. 2003; 50(7): 694-8.
- Bould MD, Crabtree NA, Naik VN. Assessment of Procedural Skills in Anaesthesia Br J Anaesth. 2009; 103(4): 472-483.
- Norris A, McCahon R. [editorial] Cumulative sum (CUSUM) assessment and medical education: a square peg in a round hole Anaesthesia 2011; 66(4): 250-254.
- Calsina L, Clara A, Vidal-Barraquer F. The Use of the CUSUM Chart Method for Surveillance of Learning Effects and Quality of Care in Endovascular Procedures
- MacKenzie Kr, Aning J. Defining competency in flexible cystoscopy: a novel approach using cumulative Sum analysis BMC Urology 2016; 16:31
- Kemp SV, El Batrawy SH, Harrison RN, Skwarski K, Munavvar M, Roselli A, Cusworth K, Shah PL. Learning curves for endobronchial ultrasound using cusum analysis. thorax.bmj.com/content/65/6/534.full.pdf
- RCOA bulletin 54 - The Royal College of Anaesthetists https://www.rcoa.ac.uk/system/files/CSQ-Bulletin54.pdf Mar 18, 2009 - A learning curve for all – CUSUM curves in initial assessment of competency. Page 13
- Komatsu R, Kasuya Y, Yogo H, Sessler DI, Mascha E, Yang D, Ozaki M. Learning Curves for Bag-and-mask Ventilation and Orotracheal Intubation: An Application of the Cumulative Sum Method Anesthesiology 2010; 112: 1525-1531.
- Ospina ODA, Medina AMR, Marulanda MC, Buitrago LMG. Cumulative Sum learning curves (CUSUM) in basic anaesthesia procedures Colombian Journal of Anesthesiology 2014; 42(3): 142-153.
CUSUM 間隔管制圖
-
Lucas JM.
Counted data CUSUM's
. Technometrics. 1985; 27(2): 129-144 - Borror CM, Kerts JB, Montgomery DC. Robustness of the time between events CUSUM. International Journal of Production Research. 2003; 41(15): 3435-3444
- Deserno M. Linear and Logarithmic Interpolation 2004-03-24 [ www.cmu.edu/biolphys/deserno]
以 HIV/AIDS 為例進行自我測試
- Adeoti OA. Application of Cusum Control Chart for monitoring HIB/AIDS patients in Nigeria International Journal of Statistics and Applications 2013; 3(3): 77-80. [ DOI: 10.5923/j.statistics.20130303.07]