用於比較機構績效的漏斗圖|陶塾醫品秘笈

✂ 什麼是漏斗圖？

漏斗圖是圖形工具，用於比較照護機構（或專業照護群體間）的臨床績效。
比較使用品質指標並挑戰標竿。
當分母差異大時，它特別有用。
y 軸上繪製了每個組的指標值，x 軸上繪製了該組的樣本量（分母）。
隨著分母樣本量的增加，管制限制變窄，從而形成特有的漏斗形狀。

當前對當責制和健康照護組織的效率的需求，再加上常規臨床照護過程和結果的數據更容易取得，導致人們更加關注健康照護監管中的統計方法。漏斗圖是一種將指標轉為可視化數據的方式。它由二個主要部分組成：漏斗圖和散布圖。 ^[1]本質上，漏斗圖就是由漏斗疊加在散布圖上所組成。

散布圖表示醫療機構的指標結果。每個點表示醫院或醫療照護區域(類似醫療網/健保局分區)的指標結果，相對於其分母大小或服務量。
漏斗是一種數學創造（也稱為統計誤差幅度），它說明了表示計算平均值（通常是全國平均值）上下 2 或 3 個標準差的邊界。
計算指標結果的分母大小（案例或服務量）當計算漏斗時要考慮；因此，小型組織的漏斗邊界較寬（即服務量較低），而大型組織的漏斗邊界較窄（即服務量較大）。

垂直軸（y軸）表示指標值。軸上方的點表示醫院或醫療照護區域指標值較高，無論指標的方向如何。對於某些指標，希望愈高愈好，相反的其他指標（例如:死亡率），更高的值不是我們想要的。

橫軸（x軸）顯示醫院服務的人數（患者數量）、居住在醫療照護區域的人數（人口普查）或可能遭遇某事件的統計預期人數（如：住院重返或住院死亡）。 x 軸上的這些分母子組按照從小到大進行排序。靠近圖表右側的點表示服務更多人的醫院（較多數量）或擁有更多居民（較大人口）的醫療照護區域。然後使用以下 `bar p` 和 `bar u` 管制圖公式為每個子組計算管制限制。

p-chart: `bar (bar p) +- z_(crit) times sqrt( {bar (bar p) times (1 - bar (bar p))}/ {n_i})`

u-chart: `bar (bar u) +- z_(crit) times sqrt({bar (bar u)}/{n_i})`

漏斗中間的水平實線代表該指標的全國值（或比較醫院群組或醫院內病房的總平均值）。

注意：漏斗圖只能提供那些具有完整的變異性度量 (包括四要素1.極差:max-min、2.四分位距、3.方差:與均值的平方距離的平均值、4.標準差:平均距離的平均) 的指標。這樣可以清楚地展示與醫院或醫療照護區域的適當規模測量相關的指標結果，以及創建漏斗圍繞全國平均水平。由上述這些原因，並非所有指標都適合創建為漏斗圖。

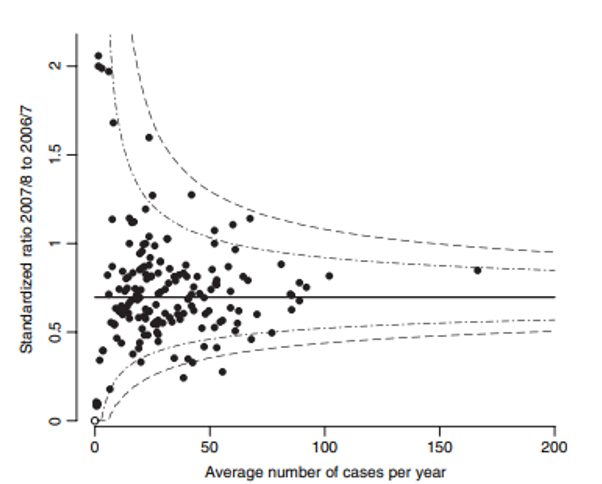
在168個信賴點中，16個點（10%）位於95%中央地區之外，相較於機率的期望值8.4(168*0.05=8.4)，3個點位於99.8%中央地區之外。

如何解釋漏斗圖？

漏斗圖阻止不適當的排名，因為它們考慮到了計算指標結果的服務量或分母。通常，較低的分子/分母指標產生的結果會比較大的分子/分母指標更易發生變化。然而，儘管服務量很大，但它們提供了在統計上高於或低於全國平均水平的指標結果的強有力的視覺指標。

在組織（醫院）完全符合標準的虛無假設下，z 值的均值為0並且SD 1，假設如果為常態性，則：

漏斗外面代表 P 值 0.001（對應於 `z_(crit)` = ± 3.10，大約 `3sigma` 的平均值）等於 99.7% 的信賴區間，並且
漏斗內部表示 P 值 0.025（對應於 `z_(crit)` = ± 1.96，大約 `2sigma` 的平均值）等於 95% 的信賴區間。

漏斗外的指標值表示調整了醫院或醫療照護區域的規模後仍是異常結果。考慮其規模，位於漏斗內的醫療照護區域或醫院的指標值結果在預期變化範圍內。要解釋指標結果與漏斗的相關，必須考慮指標的方向性。

當指標值愈低愈好（例如: 死亡率）時，可考慮將高於95%管制上限（漏斗）的醫院或醫療照護區域處於“警告(黃)區”，而高於更高的99.8%管制上限（漏斗）的醫院或醫療照護區域則處於“關注(紅)區”。這種結果可能需要進一步調查。
當指標值愈高愈好（例如，髖骨骨折48 小時內進行手術率），低於 95% 管制下限（漏斗）的醫院或醫療照護區域處於“警告(黃)區”，低於較低的 99.8% 管制下限（漏斗）的醫院或醫療照護區域則處於“關注(紅)區”。

文獻上的 p-管制圖範例

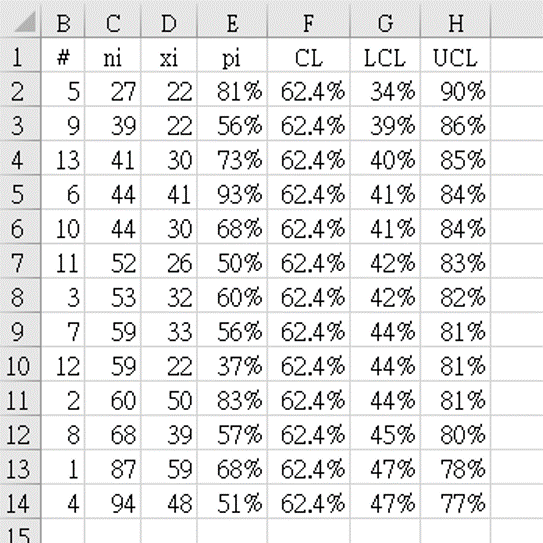
表2. 文獻中的漏斗圖示例 ^[2] : 具有漏斗限制的MRSA百分比的 p 管制圖。

參考文獻 4（表 5.9）中的數據，如上表 2 所示，將欄重命名如下：「醫院」為序列號“#”，「S. aureus金黃色葡萄球菌」的感染數量作為分母“`n_i`” 和「MRSA 的數量」作為計數“`x_i`”。表 2 顯示按子組 `n_i` (C 欄)大小排列的數據，從最小到最大。
每組的指標值 `p_i = x_i` ÷ `n_i` 在 EXCEL 中公式為 =D2/C2 複製到 E2，向下拉填E3至E14。
所有組的總平均值計算為 `bar (bar p)` "=SUM(D2:D14)/SUM(C2:C14)" = 0.62448. 這存儲在 F 欄中，該欄被標記為 CL，為管制圖的中心線。
G 欄被標記為 LCL（下管制限制），並按 p 管制圖的公式計算下限：
以G2為例： "=F2-3*SQRT(F2*(1-F2)/C2)" = 0.3490 = 34.5%
相同的方法，H 欄被標記為 UCL（上管制限制），並按 p 管制圖的公式計算上限：
以H2為例： "=F2+3*SQRT(F2*(1-F2)/C2)" = 0.90406 = 90.4%
圖 2 顯示了使用表 2 數據繪製的漏斗圖。

圖2. 文獻 <sup> [2] </sup> 中的漏斗圖範例：具有漏斗上下限的 MRSA 百分比的 p 管制圖。 — 圖2. 文獻 ^[2] 中的漏斗圖範例：具有漏斗上下限的 MRSA 百分比的 p 管制圖。

結果：
• 有 3 個代表組織的點超出限制，2 個以上（第4家、第10家）和 1 個以下（第9家）。
• 顯然，MRSA發病率的特殊原因並不僅僅發生在 Staphylococcus aureus 金黃色葡萄球菌病例較多的組織中。

區域醫院的 U 管制圖範例

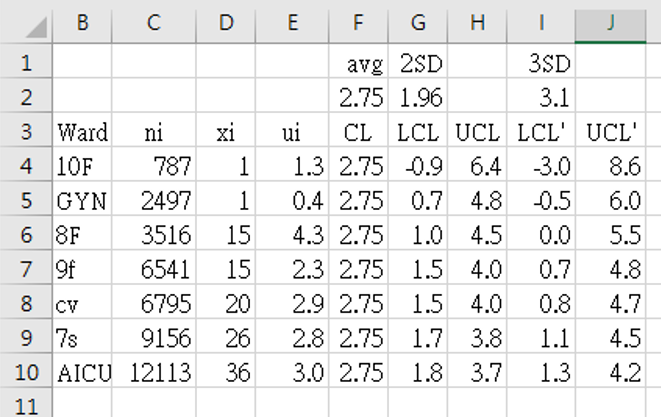
數據收集期：2019年1月1日至2021年4月30日。
上表 3 中的數據，欄如下：ward代表病房而不是順序編號，每組以該病房患者留置導尿管的總天數為分母 `n_i`，以CDC標準診斷的尿路感染總數為計數 `x_i`。表 3 顯示按子組大小（`n_i`）順序排列的數據，從最小到最大。
每個組的指標值 `u_i = x_i` ÷ `n_i` 計算公式為=1000*D4/C4直接放在E4(顯示 CAUTI 感染率為‰），公式向下複製以填滿 E 欄。
所有組的總平均值計算為 `bar (bar u)` "=1000*SUM(D4:D10)/SUM(C4:C10)" = 2.75329. 這個值存儲在 F 欄中，該列被標記為 CL，為管制圖的中心線。
欄 G （LCL）和 I （LCL'）（下管制限制）是使用 `u` 管制圖公式計算的 `z_(crit)` 值 1.96 [G2] 和 3.1 [I2]：
G4: "=$F$2-$G$2*SQRT($F$2*1000/C4)" = -0.912728 = -0.9‰
I4: "=$F$2-$I$2*SQRT($F$2*1000/C4)" = -3.045005 = -3.0‰
以同樣的方式，H 欄（UCL）和 J （UCL'）（上管制限制）也使用 `z_(crit)` 值 1.96 [G2] 和 3.1 [I2] 計算 u 管制圖的上限公式：
H4: "=$F$2+$G$2*SQRT($F$2*1000/C4)" = 6.41931 = 6.4‰
J4: "=$F$2+$I$2*SQRT($F$2*1000/C4)" = 8.55159 = 8.6‰
圖 3 顯示了使用表 3 數據繪製的漏斗圖。

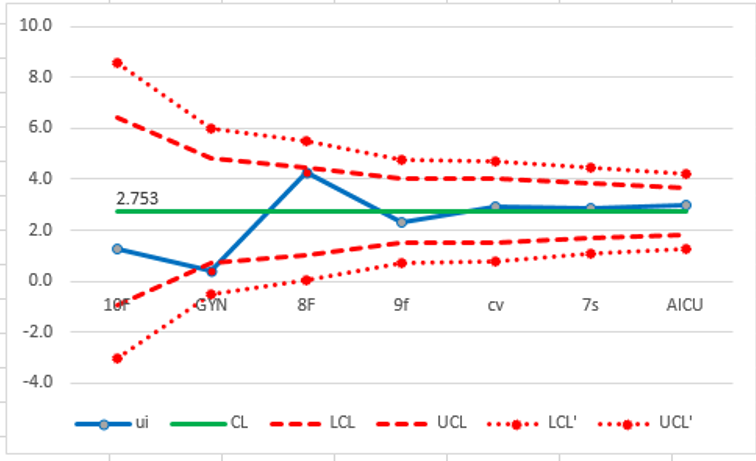
圖 3. 表 3 的漏斗圖：區域醫院病房別 CAUTI 帶漏斗上下限的 <em>u</em> 管制圖。 — 圖 3. 表 3 的漏斗圖：區域醫院病房別 CAUTI 帶漏斗上下限的 u 管制圖。

結果：
• 全院的整體 CAUTI 比率（CL）為 2.753‰。
• 所有病房都在管制上下限範圍內（GYN病房剛好在2個標準差的管制下線上）
• 此圖中沒有顯示任何特殊原因，無論導尿管使用的日子是高（7s病房）或低（10f病房）
• 嘗試改進的應針對全院的CAUTI系統管理，而不是針對任一特定病房。

區域醫院的 P 管制圖範例與團體標準相匹配

表4. 區域醫院的死亡率數據使用 <em>p</em> 管制圖公式計算漏斗上下限。 — 表4. 區域醫院的死亡率數據使用 p 管制圖公式計算漏斗上下限。

數據收集期：2017年1月1日至2021年4月30日。
上表 4 的數據，列如下：醫院別而不是順序編號，以各醫院同期住院總人數為分母 `n_i`和每組死亡總數 `x_i`。表4顯示按子組大小（`n_i`）順序排列的數據，從最小到最大。
每組指標值 `p_i = x_i` ÷ `n_i` 計算式為 =B29/C29 填入D29(將死亡率顯示為 %) 並將公式向下複製以填滿 D 欄
所有組的總平均值計算為
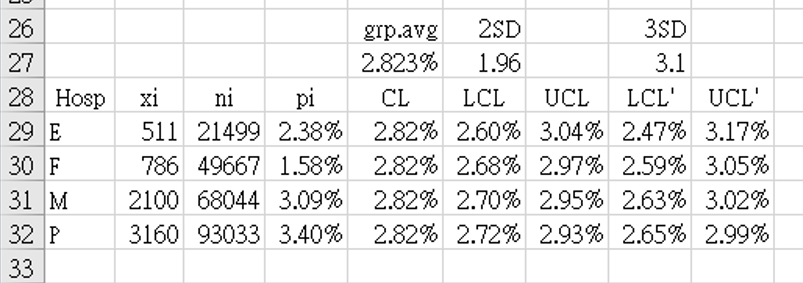
`bar (bar p)` "=SUM(B29:B32)/SUM(C29:C32)" = 2.82334%.
這存儲在欄 $E$27，並複製從 E29 到 E32 當作CL，管制圖的中心線。
欄 F （LCL）和 H （LCL'）（管制下限）是使用 `z_(crit)` 值 1.96 [F27] 和 3.1 [H27] 計算的 p 管制圖的限值公式：
F29: "=$E$27-$F$27*SQRT(($E$27*(1-$E$27))/C29)" = 2.60192% = 2.60%
H29: "=$E$27-$H$27*SQRT(($E$27*(1-$E$27))/C29)" = 2.47314% = 2.47%
以同樣的方式，欄 G （UCL）和 I （UCL'）（管制上限）是使用 `z_(crit)` 值 1.96 [F27] 和 3.1 [H27] 計算的 p 管制圖的限值公式：
G29: "=$E$27+$F$27*SQRT(($E$27*(1-$E$27))/C29)" = 3.04475% = 3.04%
I29: "=$E$27+$H$27*SQRT(($E$27*(1-$E$27))/C29)" = 3.17353% = 3.17%
圖 4 顯示了使用表 4 數據繪製的漏斗圖。

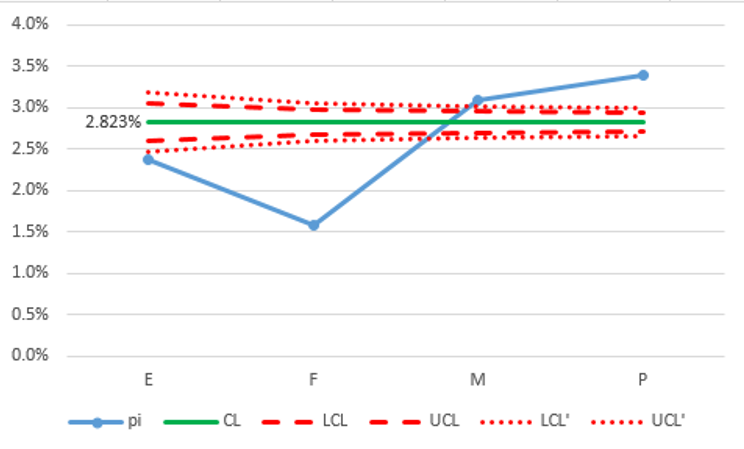
結果：
• 這4家醫院的加權平均死亡率為2.823%。此指標被解釋為越低越好。
• 所有4家醫院均因特殊原因變化：漏斗下方之外的2家醫院（E，F）（99.7%）和2家醫院（M，P）漏斗上方之外（99.7%）。
• 漏斗（UCL'）上管制線外的兩家醫院（M、P）應針對如何改善結果進行調查。
• 漏鬥（LCL'）下管制線外的兩家醫院（E， F）應考慮數據驗證，以確保其報告不會低估死亡率。
• 此圖中醫院數量少可能是管制限制存在極端差異的原因。如果更多的醫院參與分析，結果會更有說服力。

與國家標準相較量的區域醫院的P管制圖範例

表5. 區域醫院的死亡率數據使用 p 管制圖公式計算與國家標準相較量的漏斗上下限。

數據收集期：2017年1月1日至2021年4月30日。
上表 5 的數據，列如下：醫院別而不是順序編號，以各醫院同期住院總人數為分母 `n_i`和每組死亡總數 `x_i`。表5顯示按子組大小（`n_i`）順序排列的數據，從最小到最大。
每組指標值 `p_i = x_i` ÷ `n_i` 計算式為 =B4/C4 填入D4 (將死亡率顯示為 %) 並將公式向下複製以填滿 D 欄
總平均值使用來自國家數據庫醫學中心的加權平均值
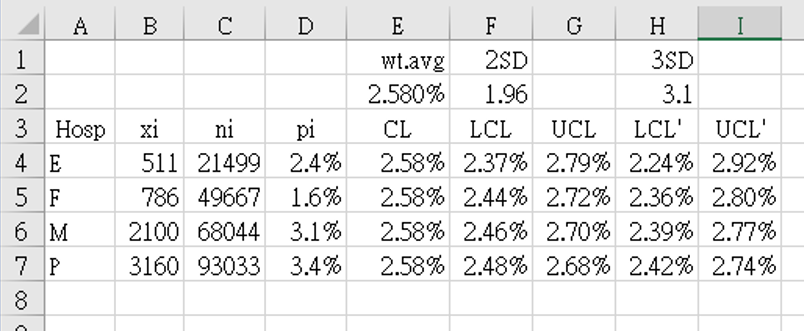
`bar (bar p)` = 2.580%
這存儲在欄 $E$2，並複製從 E4 到 E7 當作CL，管制圖的中心線。
欄 F （LCL）和 H （LCL'）（管制下限）是使用 `z_(crit)` 值 1.96 [F27] 和 3.1 [H27] 計算的 p 管制圖的限值公式：
F4: "=$E$2-$F$2*SQRT(($E$2*(1-$E$2))/C4)" = 2.36808% = 2.37%
H4: "=$E$2-$H$2*SQRT(($E$2*(1-$E$2))/C4)" = 2.36808% = 2.37%
以同樣的方式，欄 G （UCL）和 I （UCL'）（管制上限）是使用 `z_(crit)` 值 1.96 [F27] 和 3.1 [H27] 計算的 p 管制圖的限值公式：
G4: "=$E$2+$F$2*SQRT(($E$2*(1-$E$2))/C4)" = 2.79192% = 2.79%
I4: "=$E$2+$H$2*SQRT(($E$2*(1-$E$2))/C4)" = 2.91519% = 2.92%
圖 5 顯示了使用表 5 數據繪製的漏斗圖。

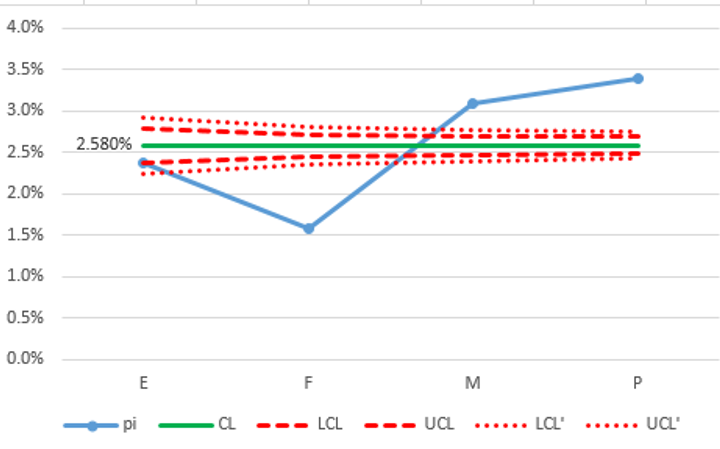
結果：
• 漏斗圖通常與國家標準進行比較（如果有此類數據）。來自國家數據庫的醫學中心加權平均死亡率 (CL) 為 2.580%。
• 雖然這個漏斗圖仍然只使用了圖 4 中的 4 家當地醫院，但在這種情況下（使用國家標準）我們不必擔心參與醫院的數量太少。計算僅使用全國平均值和每家醫院的分母，因此結果與參與或未參與的其他醫院數量無關。
• 與上一個範例一樣，超出管制下限的醫院需要先檢查其數據並排除通報不足。如果數據已經驗證，那麼E醫院可以放鬆，他們已經取得了相當於，甚至略好於國家標準的結果。如果數據已經驗證，那麼F醫院就比全國平均水準要好。在過度自信之前，他們需要考慮其他可能解釋差異的因素（例如區域人口統計和風險分層）。
• 與圖 4 相比，M 和 P 醫院都比 99.7% 的管制上限（UCL）之上的異常值更加地明顯。他們應該將品質改進計劃定位到這個指標上，看看為什麼他們的死亡率高於全國平均水準。

關鍵文獻

Canadian Institute for Health Information. Use of Funnel Plots for Reporting Indicator Results www.cihi.ca
Provost LP, Murray SK. The health care data guide. Learning from data for improvement. www.amazon.com 2011. John Wiley & Sons.
Spiegelhalter DJ. Funnel plots for comparing institutional performance. Statistics in Medicine 2005; 30;24(8): 1185-1202.
DOI: 10.1002/sim.1970 2004-11-29.
Spiegelhalter DJ, Sherlaw-Johnson C, Bardsley M, Blunt I, Wood C, Grigg O. Statistical methods for healthcare regulation: rating, screening and surveillance. J. R. Statist. Soc. A 2012; 175, Part 1, pp. 1–47