使用EXCEL計算Laney P' 及 U' 管制圖

屬性管制圖通常用於監測計數數據。計數管制圖包括「是/否」類型數據 （例如患者的體重是否在特定範圍內）和計數類型數據（如回收的滿意度調查數值）。這些屬性管制圖基於二大基礎依照（二項式或卜瓦松）分佈的假設以及分佈的平均值隨著時間的推移是相同的二大假設。這二大假設通常不正確，尤其是在樣本量較大的情況下。

對子組大小非常大的屬性數據（p、u）使用舒華特(Shewhart)管制圖的計算可能會導致圖表不是很有用（表 1，圖 1）。繪製的數據點比基於二項式（p 管制圖）或卜瓦松（u 管制圖）分佈的極限理論計算所預期的變化大得多。這個問題在健康照護應用中被稱為「過度分散」 (over-dispersion)。 ^[5] . 當使用行政資料庫的措施來研製管制圖時，這種現象經常發生。

如果 p 或 u 管制圖表的控制上下限非常窄，幾乎每個點都超出了管制限制，請使用 Laney P'管制圖（P' 發音p prime讀音）或 U'圖表 （U' u prime）來調整數據中的過度分散或分散不足。過度分散可能導致傳統計數管制圖顯示超出管制限制的點大量增加。分散不足可能導致傳統計數管制圖顯示管制限制之外的點太少。Laney P' 圖根據這些條件進行調整。

如何查證過度分散管制圖

1. 首先研製適當的計數管制圖（p或u管制圖）
2. 如果限制看起來「太窄（太緊）」，並且涉及數字非常大的子組，則尋找方法將數據進行層別法分類，例如：
   • 將月份數據分成天的子組中
   • 將數據分類到組織部門子組中
3. 如果您最終仍擁有大型子組大小和充滿特殊原因的圖，請花時間與主題專家一起試圖識別和理解特殊原因

傳統 p 管制圖範例（二項分佈）

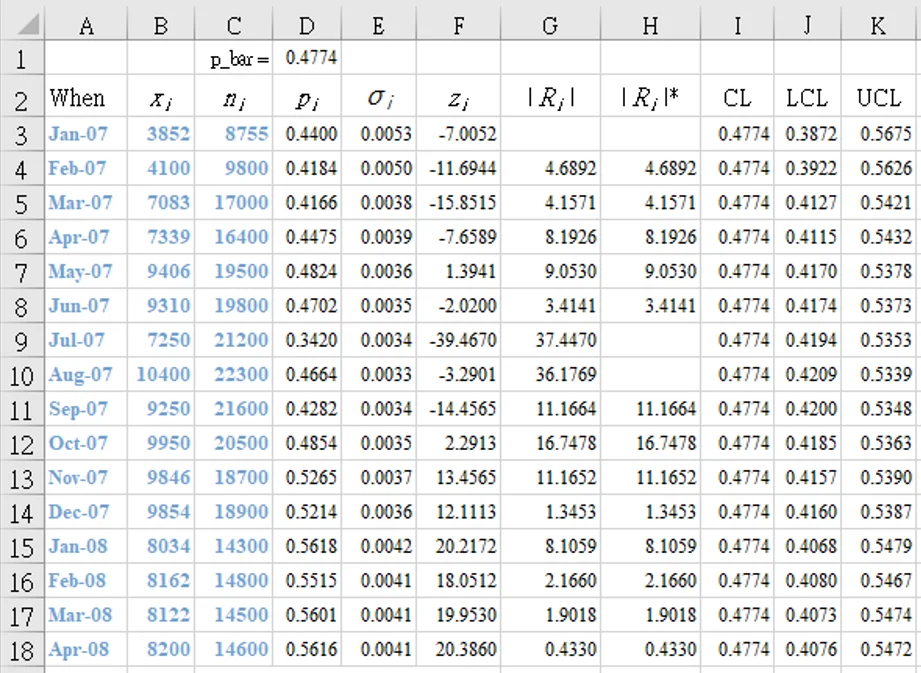
表1顯示數據來自健康照護組織的預約中心。 ^[4] . 該表給出了每月通過電話與健康照護中心預約的患者人數（`x_i`），以及該健康照護組織當月註冊的患者總數（`n_i`）。每個月（子組）由連續的指數編號表示，該指數編號相關參數顯示為下標（`i`)。計數從 1 開始，到總共 16 個子組 （`k`） 。

1. 計算每月電話預約百分比。
   將公式複製到所有D欄
   `p_i = ((x_i/n_i) times mf)` 其中「`mf`」= 乘法因子
   例如： [D3] "=(B3/C3)*1" ←`mf`=1 （輸入公式時忽略引號）
2. 計算每月電話預約率的平均值（`bar p`），並將公式複製在M1這個欄位
   `bar p = frac {sum_(i=1)^k(p_i)}{k}`
   [M1] "=SUM(D3:D18)/`k`"
3. 計算二項分布的標準差。
   將公式複製到E3欄，向下拉填滿所有E欄
   `sigma_p = sqrt(frac{bar p ((1 times mf) - bar p)}{n_i})` 其中「`mf`」= 乘法因子
   例如： [E3] "=SQRT($M$1*((1 * `mf`)-$M$1)/C3)"
4. 標示CL(中心線)用平均電話預約率填滿F欄(就是M1的值)
   `0.4774`
5. 計算每月下管制線(LCL)，因為每月掛號總人數 `n_i` 有變。
   複製公式至G3欄，向下拉填滿所有G欄
   `LCL = bar p - 3 sigma_p`
   例如： [E3] "=F3-3*E3"
6. 計算每月下管制線(UCL)，因為每月掛號總人數 `n_i` 有變。
   複製公式至H3欄，向下拉填滿所有H欄
   `UCL = bar p + 3 sigma_p`
   例如： [E3] "=F3+3*E3"
7. 選取A欄(X軸座標),選取D欄（`p_i`）, F欄(CL), G欄 (LCL), H欄(UCL)得到折線圖
   如圖1

表1. 屬性 p 管制圖傳統計算的數據系列

 

圖1. 屬性 p管制圖使用表1數據

結果：

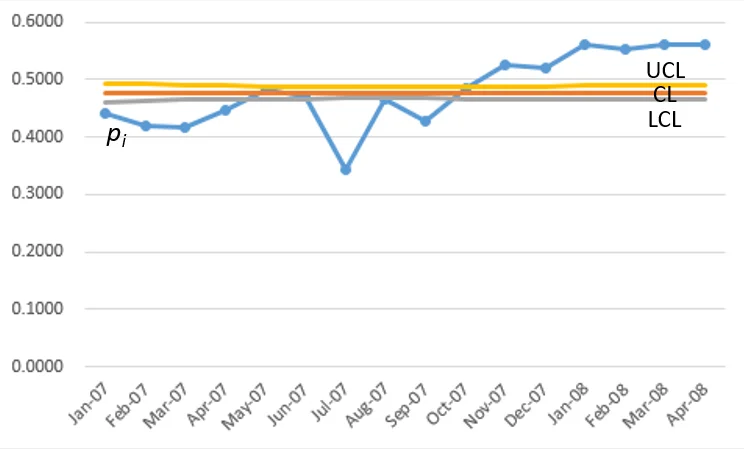
• 管制下限與上限（LCL，UCL）非常狹窄，聚集在中心線附近（CL）
• 幾乎所有數據點都超出了管制線外

=> 言下之意暗示此為一個非常失控的系統，或者更確切地說，這種情況，此圖沒有幫助解釋。

修改：
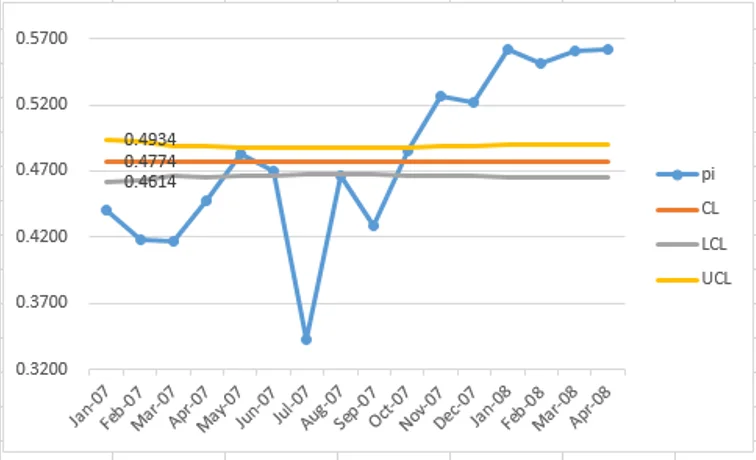
即使我們將 y 軸的尺度調整從0.32至 0.58（圖1a），以聚焦於控制限制之間的區域，結果也是一樣的：這種狹窄的管制限制導致大多數數據點超出上、下限範圍。
（謹防！）使用非零起點的話 y 軸不適合品質改進數據，因為它會產生誤解的可能性。與本範例一樣，當 y 軸被限制為僅略高於下限時，LCL 和 UCL 之間的間隙看起來「有意義」（圖 1a： 0.32 ~ 0.58），但在正確查看數據時，從零開始的 y 軸（圖 1），傳統的管制限制非常狹窄，無助於解釋所研究系統中的性能表現。

詮釋
管制圖將子組內的變化與子組間的變異進行比較。範例（圖 1）顯示月內變化小於月間變化。
發生這種情況的一個原因是子組大小較大。請注意，`n_i`值位於管制限制的分母中。因此，隨著`n_i`變大，管制限制（LCL，UCL）越來越接近：這就是為什麼這麼多點超出了管制範圍

圖1a. 計數p管制圖使用表1數據但起始點y軸不是0

表2. 對屬性 `p` 管制圖進行 Laney 調整的數據系列

 

圖2. Laney `p'` 管制圖使用表2的數據

結果：
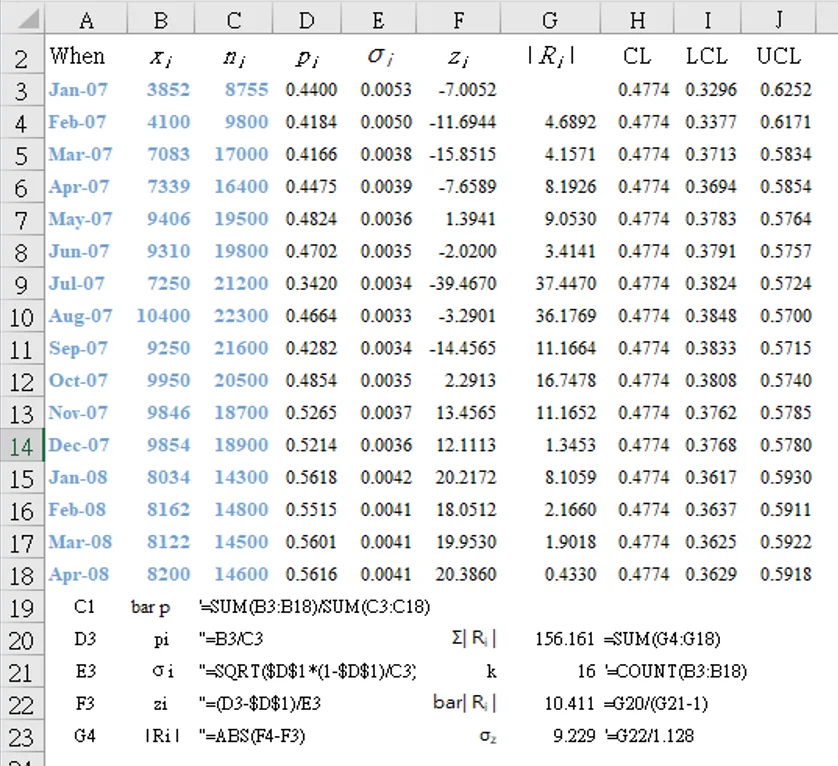
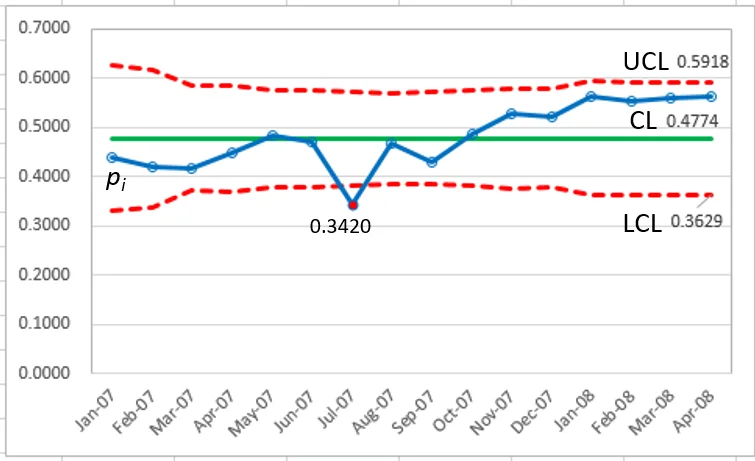
比較管制限制方程 `p` 管制圖和Laney `p′` 管制圖。唯一的不同的地方是 `p^'` 管制圖上的 `sigma_z`。現在的數據表明，只有第7點超出管制限制之外。
`sigma_z = 9.229 ` (>1.0) 表示過度分散！

Laney 描述`sigma_z` ^[7]
這是過程變化的相對數量，而不是僅僅由二元假設來解釋的。隨著 `n_i` 的增加，由於抽樣引起的變化減少，從而使批次之間的分量相對較大。這就是為什麼具有大計數子組的應用程式經常顯示這種情況的原因。

何計算 Laney `p'` 管制圖通過從移動範圍中刪除極端數值

與上述程序相同（表2，圖2），但步驟5添加（'特殊原因的篩選，並從移動範圍清單中刪除'）如參考文獻Provost所述 (p156-7)。 ^[4]
計算上管制線[UL_MR] (用於XmR圖表中的移動範圍) ^[6]

mR 管制圖表沒有下限，因為移動範圍的邏輯最低值為零。管制上限 [UL_MR] 是平均移動範 `bar R^'` 圍乘以 3.27。 這個值 3.27 將是您要代入的常數值。    它是一個統計學上產生的常數，使上管制線大致相當於平均移動範圍的3個標準偏差。換句話說，它確保上範圍限制準確描述移動範圍值的常規變化。

5. 篩選特殊原因並從移動範圍行表中刪除，如下所示：
   1. 求刪除的切點值 UL_MR `= 3.27 times bar R^' = 34.0432`
   2. 刪除任何大於 UL_MR 的移動範圍;即以下兩個：(`i_7` 與 `i_8` 插入 H 欄)
      ` i=7, | R_7 | = 37.4470`
      ` i=8, | R_8 | = 36.1769`
   3. 重新計算平均移動範圍 `bar R^'` ；求H欄總和，但 `i_7` 與 `i_8` 要留空白，這二點的值已被刪除（參閱表3） `bar R^'`
      `sum_(i=2)^k | R_i | ` = SUM(H3:H18) = 82.537
      `k^' ` = COUNTIF(H3:H18,">0") = 13
      `bar R^' = frac{sum_(i=2)^k | R_i | }{k^'} = 82.537/13 = 6.349`
      (重新計算應該只進行一次)
6. 代公式計算 `z` 值的標準差
   `sigma_z = frac{bar R^'}{1.128} = 6.349/1.128 = 5.629`
   `sigma_z = 5.629 ` (>1.0) 表示過度分散！
7. 計算 `p'` 管制圖的上下限
   `CL = bar p` （與原始 p 圖表相同）
   `LCL = bar p - 3 sigma_(p_i) sigma_z`
   `UCL = bar p + 3 sigma_(p_i) sigma_z`

表3. 對屬性 p 管制圖表進行 Laney 調整的數據系列

 

圖3. Laney `p'` 管制圖使用表3數據

結果：
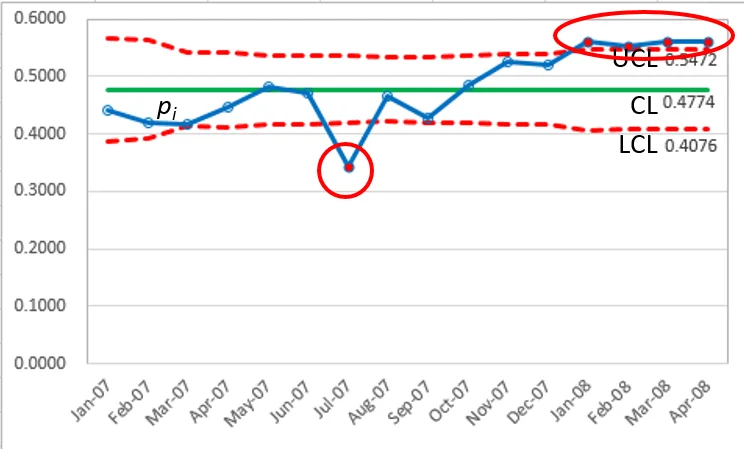
`p_7 = 0.3420 ` (低於下管制線LCL)
`p_13 ~ p_16 ` (四個點高於上管制線 UCL)
請注意，如果不應用移動範圍校正，該系列的最後四點將被解釋為控制（圖 2）。
`sigma_z = 5.629 ` (>1.0) 表示過度分散！

傳統的屬性 `u` 管制圖

請參閱文獻8範例演練（表 4，圖 4） ^[8]
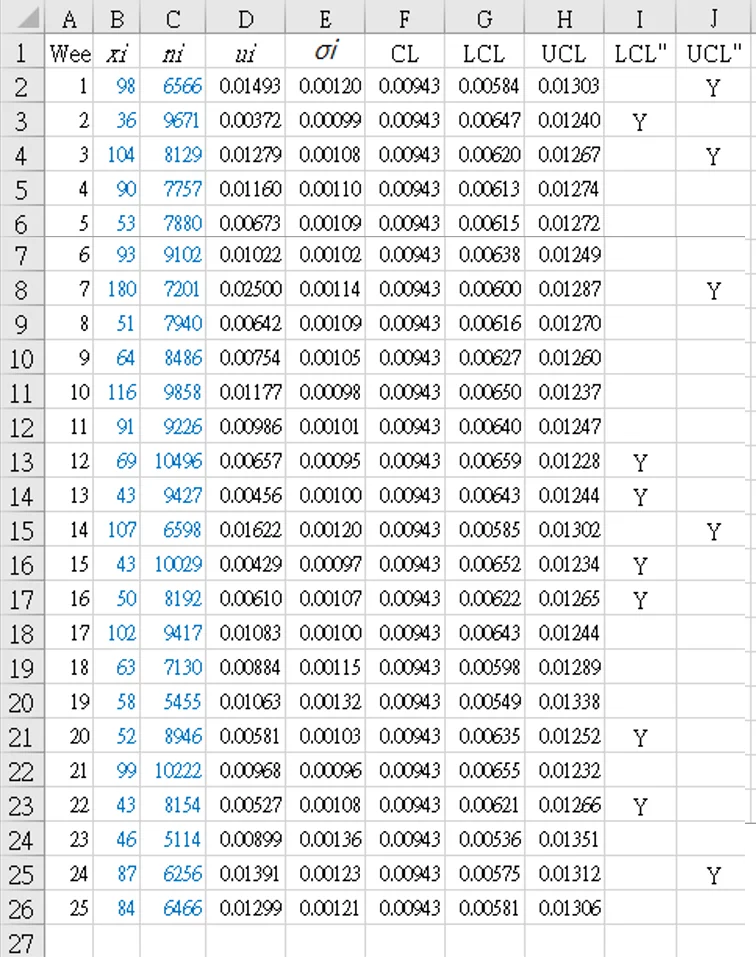
一個跨醫院小組正在監測給患者服用的藥物的錯誤率。每週記錄的數據資料是給藥的患者數量 （`n_i`） 和錯誤數 （`x_i`） 。錯誤可能包括給藥劑量錯誤、未給藥等。 25 週的數據如表 4 所示。

1. 計算整體錯誤率的平均值（`bar u`），並存儲在任何空單元格中（例如，[M1]）：
   `bar u = ({sum_(i=1)^k x_i}/{sum_(i=1)^k n_i} times mf )` 其中「`mf`」= 乘法因子
   [M1] "=(SUM(B2:B26)/SUM(C2:C26))`times`1" = 0.00943
2. 計算每週錯誤率（`u_1`），並將結果填入 D 欄，下拉公式填滿至D26
   `u_i = x_i / n_i`
   [D2] "=B2/C2" = 98/6566 = 0.01493
3. 計算每周傳統 `u` 管制圖的標準差（`sigma_(u_i)`），並填寫 E 欄，結果如下：
   `sigma_(u_i) = sqrt(frac{bar u}{n_i})`
   [E2] "=SQRT($M$1/C2)" = SQRT(0.00943/6566) = 0.00120
4. 用平均值`bar u`(CL)填滿 F 欄
   [F2~F26] "= $M$1" = 0.00943
5. 填滿傳統 `u` 管制圖下管制限制（LCL）G欄，每行各不相同：
   `LCL_(u_i) = bar u - 3 times sigma_(u_i)`
   [G2] "=$M$1-3*E2" = 0.00584
6. 填滿傳統 `u` 管制圖上限 （UCL）H欄，每行各不相同：
   `UCL_(u_i) = bar u + 3 times sigma_(u_i)`
   [H2] "=$M$1+3*E2" = 0.01303
7. 使用 I 和 J 欄檢查積分是否超出控制限制：
   [I2] "=IF(D2<G2,"Y","")"
   [J2] "=IF(D2>H2,"Y","")"

表4. 傳統計算的屬性 `u` 管制圖數據系列

 

圖4. 使用表 4 中的數據畫屬性 u 管制圖

結果：
使用欄 I 和 J 檢查積分是否超出控制限制：
低於下管制線的週別： 2, 12, 13, 15, 16, 20, 22
高於上管制線的週別： 1, 3, 7, 14, 24

`u^'` 管制圖Laney計算

`i` 點的 `z` 值計算如下：

1. 複製表 4 的 A~H 欄所有資料至新工作表，並新增插入欄位 F(`z_i`), G (|`R_i`|), and H ( |`R_i`|*)並命名為表5(表 4 的 F,G,H 欄因為插入新欄故表5已變成 I,J,K 欄)
2. 使用與 Laney p' 管制圖相同的步驟，確認以下計算
   
   `bar u ` [P1]: "=SUM(B2:B26)/SUM(C2:C26)" → `0.00943`
   `bar R` [P2]: "=AVERAGE(G3:G26)" → `5.07597`
3. 篩選特殊原因並從移動極差欄表中刪除
   
   UL_MR [P3]: "=3.27*$P$2" → `16.59844`
   G 欄中沒有值（|`R_i`|）超過 UL_MR，因此 H 欄（|`R_i`|*） 是重複的，不會影響下一步驟。
4. 計算此資料的 z 標準差值，並比照 Laney p' 管制圖相同的步驟重新計算上、下管制線：
   
   `sigma_z` [P4]: "=$P$2 ÷ 1.128" → `5.07597/1.128 = 4.49997`

表5. 對屬性 `u` 管制圖進行 Laney 調整的數據系列

 

圖5. 使用表 5 的數據的 Laney `u'` 管制圖

結果：
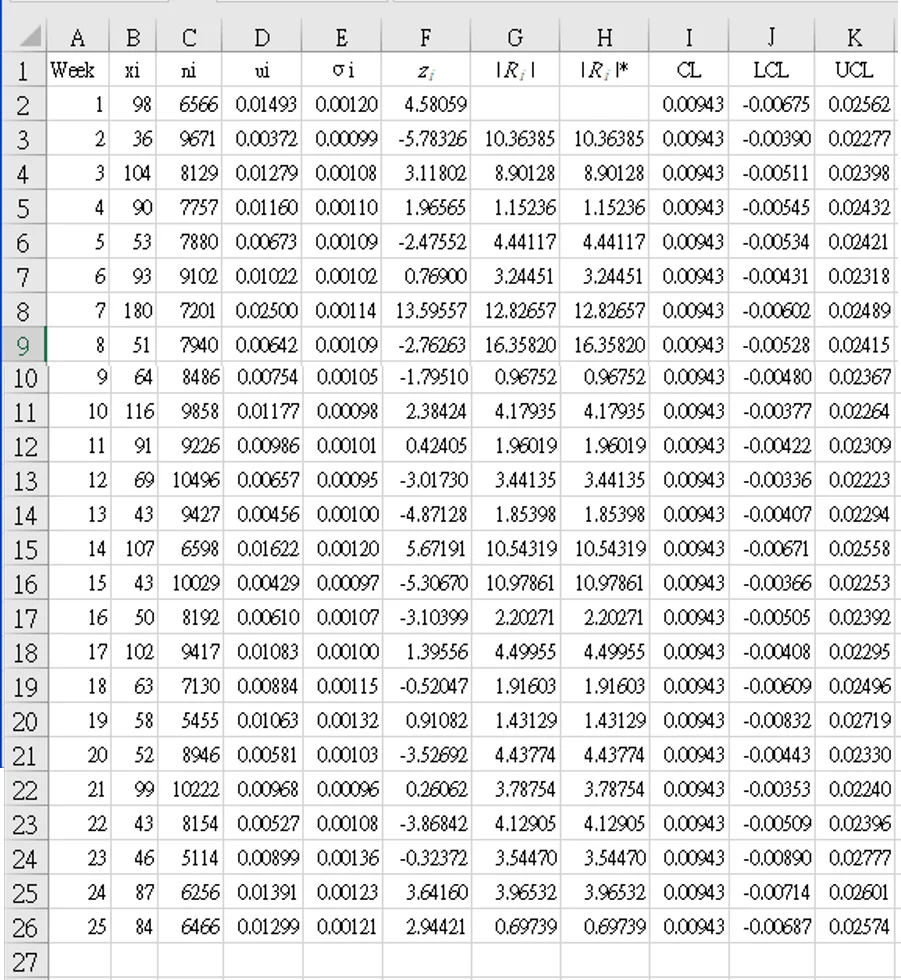
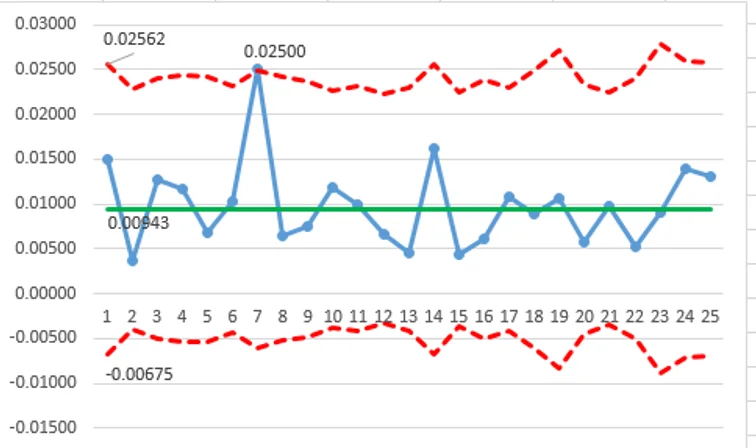
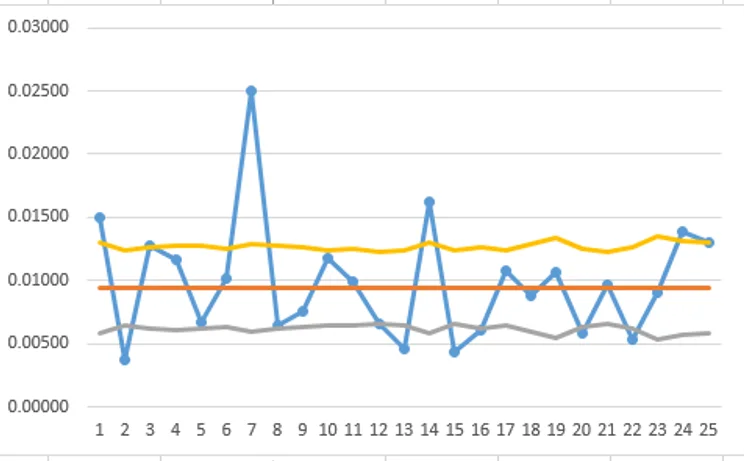
只有一個點（`u_7=0.02500`）超出上管制限制（>UCL）。
`sigma_z = 4.49997 ` (>1.0) 表示過度分散！
此圖的 LCL 值低於零僅顯示用於演示目的（以顯示所有計算的結果）。管制下限不能低於零，在此圖的發行版本中，零以下的 LCL 值應全部調整為零！

文獻中的其他例子

對於那些熟悉 R 語言的人，雅各·安海傑 ^[9] 對品質改進管制圖有非常詳細的解釋。這個 qicharts2 程式包包含兩個主要功能，用於分析和可視化數據以實現持續品質改進：使用的指令是 qic()和 paretochart()。最後一個範例圖（案例 5） 使用 nhs_accidents 數據集來演示 p prime 管制圖的使用。nhs_accidents 數據集包含執勤後 4 小時內就診的急診患者人數。樣本量非常大（>250,000）。

Laney 指出，當不存在過度分散時，p’ (u’)管制圖表將給出與傳統圖表相同的結果，Laney 建議有比例和比率時直接使用 p’(u’)管制圖。

圖6. 執勤後 4 小時內就診的患者比例（Laney p' 管制圖）。 ^[9]

關鍵文獻

1. Laney DB. A New Control Chart: Laney P’ Chart YouTube Pyzdek Institute, 2019 May 2.
2. Laney DB. Improved Control Charts for Attributes Quality Engineering 2002; 14(4): 531-537.
3. Mohammed MA, Laney DB. Overdispersion in health care performance data: Laney's approach Qual Saf Health Care 2006; 15(5): 383-4.
4. Provost LP, Murray SK. The health care data guide. Learning from data for improvement. www.amazon.com 2011. John Wiley & Sons.
5. Minitab 18 Support. Overdispersion and underdispersion. support.minitab.com/.../overdispersion-and-underdispersion [Accessed 2021-07-12]
6. Barr S. Chapter 10. XmR Chart Instructions www.staceybarr.com [Accessed 2021-07-14]
7. McNeese B. Laney p' Control Chart www.spcforexcel.com/.../laney-p-control-chart [Accessed 2021-07-12]
8. McNeese B. Laney u' Control Chart www.spcforexcel.com/.../laney-u-control-chart [Accessed 2021-07-12]
9. Anhøj J. Quality Improvement Charts. An implementation of statistical process control charts for R anhoej.github.io/.../qicharts2.html [Accessed 2021-07-12]