使用推移圖改善品質
在品質改進專案期間監測改變的影響建立推移圖是好方法,一開始可用初始中位數當作基線。如果取得基線資料的過程來自顯示沒有括弧內指(位移、趨勢、資料線群數、天文資料點)的這些信號,則將此初始中位數擴展到或「凍結」到未來。這樣,新資料才不會影響初始中位數。新資料的任何變化都更清楚地與基線中位數相對立,從而可以更準確地檢測改進信號(基於概率的規則相對於此中值)。
位移和資料線群數規則在適用之前需要超過 10 個點。但是,有許多應用(例如,對年度 PSA 測試的患者監控),推移圖僅使用三個或四個資料點,便可及早預測中心趨勢和趨勢。
推移圖的局限性
推移圖旨在早期偵測過程中隨時間而改善或退步的信號。
但是,如果流程是穩定的(和 Shewhart 關聯的管制圖定義),則推移圖無法確定。將管制圖與推移圖一起使用可能會造成混淆,因為兩種方法分別包含不同規則用於識別非隨機模式的。使用推移圖時,請避免使用「特殊原因」和「穩定」或「不穩定」等用語,相反地可用於管制圖。
如何建構推移圖
- 推移圖(運行圖、趨勢圖)是按某種順序來繪製數據資料的圖形顯示。
- 水平軸通常是時間刻度(例如天、周),但也可能包括有順序別的患者、訪問或流程。
- 垂直軸表示正在研究的品質指標(例如感染率、患者跌倒次數、再入院率)。
- 通常,我們以中位數作為圖形中心線,因為:
- 它提供了一半的觀測值預期位於中心線上方和下方的點,以及
- 中位數不受資料點極值的影響
- 目標線、執行措施時間點以及其他事件的註釋也可以添加到推移圖中。
中位數和推移圖規則可幫助我們目視化不同干預措施、變化、測試其隨時間變化而產生的影響。
説明解釋推移圖的規則
三個以概率為基礎的規則,用於客觀地分析推移圖:基於 p<0.05 的 α 誤差分析資料中非隨機模式的證據。
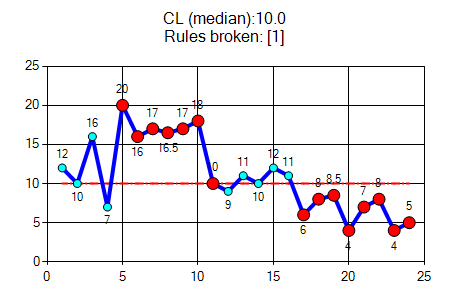
規則-1 — 位移(shift)
|
六個或更多連續點,要麼全部高於中位數,要麼全部低於中位數。落在中位數的值不會增加不會中斷飄移。跳過落在中位數上的所有值並繼續計數。 |
|
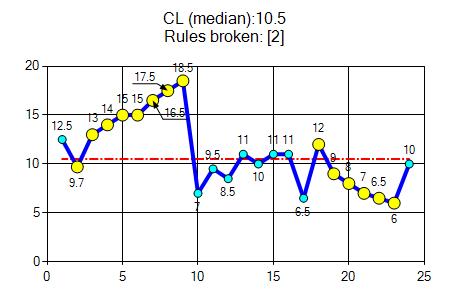
規則-2 — 趨勢(trend)
|
五個或更多連續點全部上升或全部下降。如果兩個或兩個以上連續點的值相同,則僅計算第一個點而忽略重複值;相似的值不會形成或破壞運行。 |
|
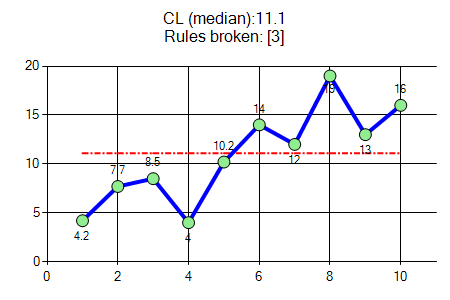
規則-3 — 資料線群數或資料點連線跨越次數(runs)
一個資料線群數是指中位數一側連續的一系列點有多少組。非隨機模式的特徵是明顯太少或太多的資料線群數來判斷,也可以用資料連線通過中線的交叉次數+1來獲得(crossings)。
一個資料線群數是指中位數一側連續的一系列點有多少組。非隨機模式的特徵是明顯太少或太多的資料線群數來判斷,也可以用資料連線通過中線的交叉次數+1來獲得(crossings)。
- 計算次數:將資料點連接起來的線數一數穿過中位數的交叉點,然後無條件加一。
- 例如,在圖#3「例外規則[3]」中,藍色資料線由 10 個資料點組成,並且此連接後的資料線僅穿過中位數一次(點 5 和點 6 之間)。
- 再加一。測試的「交叉次數 n」為「n = 1 + 1 = 2」。
- 與表 1 (本頁底部)進行比較,以確定是否存在太多或太少的資料線群數。表1顯示了如果資料是隨機分佈的,預期交叉點數;該數字顯示為從「下限 (LL)」到「上限 (UL)」的範圍。
- 以 n = 10說明,下限為 3,上限為 9;也就是說,如果此資料數列符合隨機結果測試,交叉次數應介於 LL 和 UL (3~9) 之間。
- 但是,n=2(超出範圍 3~9),因此得出的結論是資料不是隨機分佈的。
- 對於我們的品質改善監測,這意味著改變可能是行動的結果導致。
✂
規則-3:run (資料線群)
「資料線群」是中位數一側連續的一系列點。
使用在確定數據是否隨機分佈時。
「資料線群」是中位數一側連續的一系列點。
使用在確定數據是否隨機分佈時。
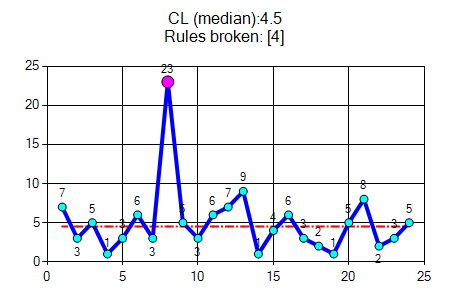
規則-4 — 天文資料點(astronomical point)
天文資料點是明顯不同于其他點的資料點。天文點不應與每個推移圖將具有的最高或最低資料點混淆。雖然規則 1、2 和 3 基於概率,但規則 4 是主觀的,並且認識到在推移圖表中直觀地顯示資料的重要性。
天文資料點是明顯不同于其他點的資料點。天文點不應與每個推移圖將具有的最高或最低資料點混淆。雖然規則 1、2 和 3 基於概率,但規則 4 是主觀的,並且認識到在推移圖表中直觀地顯示資料的重要性。
關鍵文獻
- Provost LP, Murray SK. The health care data guide. Learning from data for improvement. www.amazon.com 2011. John Wiley & Sons.
- Perla RJ, Provost LP, Murray SK. The run chart: a simple analytical tool for learning from variation in healthcare processes. wwwncbi.nlm.nih.gov BMJ Qual Saf 2011; 20: 46-51.
- Hart MK, Hart RF. Statistical process control for health care. 2000 www.amazon.com
附錄
表1、在推移圖上檢查運行次數(runs)是否太多或太少。
• NN = 推移圖上不落在中位數上的數據點總數
• LL = 資料線群數的下限(小於此次數為「太少」)
• UL = 資料線群數的上限(超過此資料線群次數為「太多」)
• NN = 推移圖上不落在中位數上的數據點總數
• LL = 資料線群數的下限(小於此次數為「太少」)
• UL = 資料線群數的上限(超過此資料線群次數為「太多」)
| NN | LL | UL | NN | LL | UL | NN | LL | UL | NN | LL | UL | NN | LL | UL | NN | LL | UL |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 10 | 3 | 9 | 20 | 6 | 16 | 30 | 11 | 21 | 40 | 15 | 27 | 50 | 19 | 33 | 60 | 24 | 38 |
| 11 | 3 | 10 | 21 | 7 | 16 | 31 | 11 | 22 | 41 | 15 | 27 | 51 | 20 | 33 | |||
| 12 | 3 | 11 | 22 | 7 | 17 | 32 | 11 | 23 | 42 | 16 | 28 | 52 | 20 | 34 | |||
| 13 | 4 | 11 | 23 | 7 | 17 | 33 | 12 | 23 | 43 | 16 | 28 | 53 | 21 | 34 | |||
| 14 | 4 | 12 | 24 | 8 | 18 | 34 | 12 | 24 | 44 | 17 | 29 | 54 | 21 | 35 | |||
| 15 | 5 | 12 | 25 | 8 | 18 | 35 | 12 | 24 | 45 | 17 | 30 | 55 | 22 | 35 | |||
| 16 | 5 | 13 | 26 | 9 | 19 | 36 | 13 | 25 | 46 | 17 | 31 | 56 | 22 | 35 | |||
| 17 | 5 | 13 | 27 | 10 | 19 | 37 | 13 | 25 | 47 | 18 | 31 | 57 | 23 | 36 | |||
| 18 | 6 | 14 | 28 | 10 | 20 | 38 | 14 | 26 | 48 | 18 | 32 | 58 | 23 | 37 | |||
| 19 | 6 | 15 | 29 | 10 | 20 | 39 | 14 | 26 | 49 | 19 | 32 | 59 | 24 | 38 |