
|
= "x-bar" 算術平均數(平均值) |

|
= "x-double-bar" 總平均值(所有平均值的平均值) |
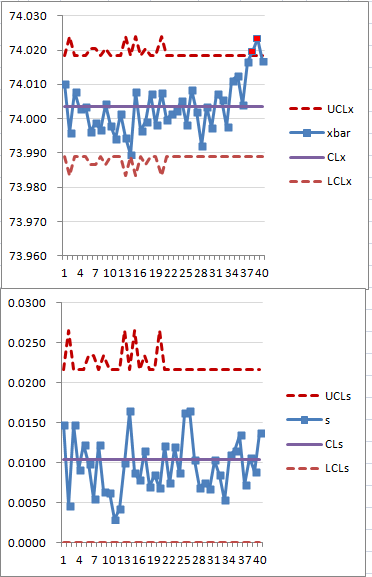
平均值與標準差管製圖是成對出現的獨立管制圖,一個是依據每個子群組的衡量結果的平均值(xbar),一個是依據分散程度(標準差)。這兩種變數通常隨時間註記。圖的中線分別為總平均值(平均值的平均值)及標準差的平均值。
觀察值的數據會儘可能依據同質性(子群組內的資料儘可能是很類似的)整合至子群組。子群組是一組在類似條件下或在相同的時間週期內取得的測量結果。子群組的大小是多變的,可以低至2或3;也可以是非常大的,如在管理性的資料庫內。
隨著子群組大小的不同,管制界線會隨之上下波動,對於樣本較小的子群組,管制界線較寬。這在 s 圖也有此現象,隨著子群組大小不同而改變。
變數管制圖的因子
>因子 {A3}、{B3}、{B4} (依據子群組的大小) 列在表二。對使用 Excel 的人,能使用 LOOKUP 指令讀取手工編碼表,亦可利用表一在 Excel 中依據子群組的大小進行運算。{C4} 因子常伴隨著 n,強調隨著子群組的大小而改變,這裡的 n ≥ 2。
解釋
使用時間資料進行流程改善,對於其他管制圖的檢測方法亦可以應用於x-bar管制圖。然而,只有檢測條件 #1(一個或更多資料點超過3個標準差的範圍)被採用。平均圖(上圖)指出抽樣間流程的變化。 標準差圖(下圖)顯示每次抽的樣本內之變異性。
當分析這些圖時,應該先分析標準差圖。如果他有一個或多個點超出管制界限,就不要進一步分析平均圖。這是因為標準差的平均值是用來計算平均圖的界限。如果標準差圖超過管制界限,則平均圖的管制上限及下限將會偏移。也要注意標準差圖沒有分區(如 1SD、2SD、3SD),因為分區不適用。
對於流程管制,只有檢測條件 #1 可用在 x-bar 和 s 圖。
那麼,繪製了這個圖該怎麼辦?你已經知道幾件事:
- 流程在管制內(穩定)
- 一般來說,未來在執行流程大約需花掉 CL(平均)的時間,除非
- 一些事情產生特殊原因變異
- 採取介入行動及啟動流程改善措施
- 使用此數據回饋給流程的使用者,特別是如果他們抱怨流程耗很多時間或總是被改變。 如果他們認為目前流程的平均是不可接受的,那基本的作法是〝採取行動改變流程!〞
如果你決定採取行動以改善穩定流程,由以下幾個現象視為流程改善的佐證:
- 降低流程的變異(亦即管制下限及管制上限的區間縮小)
- 且/或流程平均比先前程度高或低
為了檢測介入策略的影響,你利用原先的管制界限及流程平均,接著持續畫上新的資料。如果你的介入策略有效,你會看到流程的變異降低且/或偏移。
不平等的分組大小時,如何繪製平均值與標準差管制圖

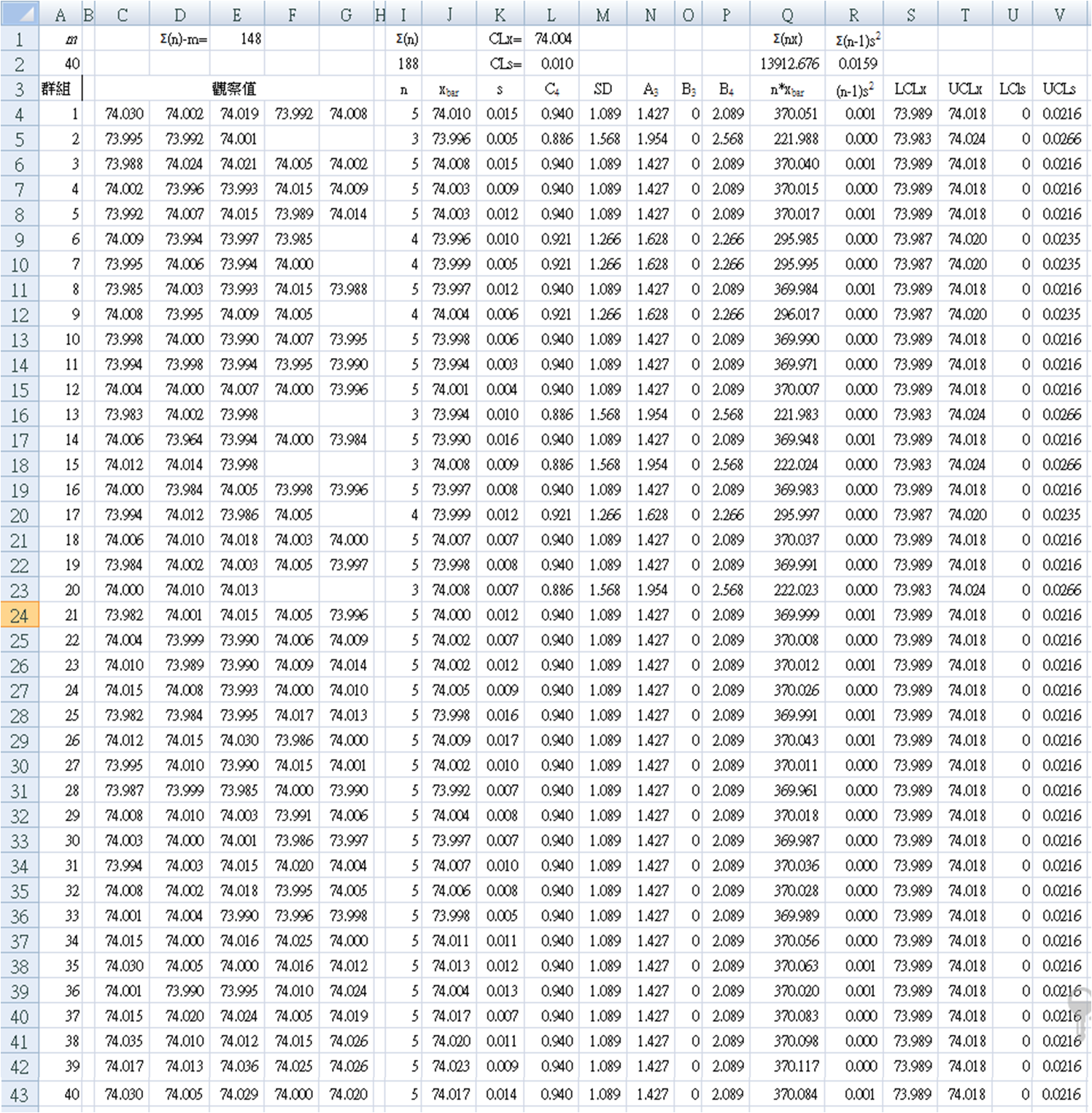
階段一:衍生因子 {A3}、{B3}、{B4}
- 每列使用 Excel 函數利用子群組的樣本數量(ni)計算子群組的平均值(xi)及其標準差(si)
將 ni 輸入工作表的欄 Hi 公式為 "=COUNT(Ci : Gi)"
→ I4 = COUNT(C4 : G4) => 5
將 xbari 輸入工作表的欄 Ii 公式為 "=AVERAGE(Ci : Gi)"
→ J4 = AVERAGE(C4 : G4) => 74.010
將 si 輸入工作表的欄 Ji 公式為 "=STDEV(Ci : Gi )"
→ K4 = STDEV(C4 : G4) => 0.015
確認公式輸入正確:舉例來說,螢幕上的第一個子群組應該輸為 n1 => 5, xbar1 => 74.010, s1 => 0.015 - 下一個欄位(L4),應針對此子群組插入 計算 {C4} 因子的公式:
= EXP(GAMMALN(Ii / 2)) * SQRT(2 / (Ii - 1)) / EXP(GAMMALN((Ii - 1) / 2))
確認子群組 #1 的公式計算的結果為 C4(n=5) => 0.940.
= EXP(GAMMALN(I4 / 2)) * SQRT(2 / (I4 - 1)) / EXP(GAMMALN((I4 - 1) / 2)) - 接著,為了簡化計算,將從 {C4} 衍生而來的標準差輸入鄰近的細格(M4)
= 3 * SQRT(1 - POWER(Li , 2)) / Li
→ M4 = 3 * SQRT(1 - POWER(L4, 2)) / L4 => 1.089 - 然後,將右邊的連續三個細格(N、O、P),使用方程式來計算 {A3}、{B3} 及 {B4}。
{A3} in Ni = 3 / (Li * SQRT(Ii))
→N4 = 3 / (L4 * SQRT(I4)) => 1.427 (對於分組 #1)
{B3} in Oi = IF((1 - Mi) < 0, 0, (1 - Mi))
→O4 = IF((1 - M4) < 0, 0, (1 - M4)) = 0 (對於分組 #1)
{B4} in Pi = 1 + Mi
→ P4 = 1 + M4 => 2.089 (對於分組 #1)
階段二:計算子群組大小不同的 CL、UCL 及 LCL
- 每行計算 [ni * xbari] 和 [ni - 1) * si2]
(a) 在工作表的欄 Qi 計算 ni * xbari = Gi * Hi
→ Q4 = I4 * J4 => 370.51
(b) 在工作表的欄 Ri 計算 R (ni - 1) * si2 = (Ii - 1) * POWER(Ki, 2)
→ R4 = (I4 - 1) * POWER(K4, 2) => 0.00087 (≅ 0.001) - 使用 A 確認子群組的數量並使用 H 欄位計算子群組總樣本數:
(a) 子群組的數量 (m) 輸入在工作表的欄 $A$2
m: A2 = COUNT(A4 : An) = COUNT(A4:A43) => 40
(b) 子群組樣本的總數輸入在工作表的欄 $I$2
I2 = SUM(I4 : In) = SUM(I4:I43) => 188
(d) Q 欄加總,並在 $Q$2 輸入 Σ[ni * xbari]
→ Q2 = SUM(Q4:Q43) => 13912.676
(e) R 欄加總,並在 $R$2 輸入 Σ[ni - 1) * si2]
→ R2 = SUM(R4:R43) => 0.0159 - 計算 xbar 的加權平均值: → L1 = $Q$2 / $I$2 => 13912.676 / 188 => 74.004

- 計算 s 的加權平均值: → [Σ(ni) - m] : E1 = I2-A2 => 188 - 40 => 148

→ L2 = POWER($R$2/$E$1, 0.5) = POWER(0.0159 / 148, 0.5) = 0.010 - 計算 x 圖每個子群組的中線及管制界限
CLx (x-double-bar) = L1 = 74.004
LCL(n=i) , UCL(n=i) = CLx ± A3(n=i) * CLs
LCL(n=1): S4 = $L$1 - N4 * $L$2
→ S4 = 74.004 - 1.427 * 0.010 => 73.989
UCL(n=1): T4 = $L$1 + N4 * $L$2
→ T4 = 74.004 + 1.427 * 0.010 => 74.018 - 計算 s 圖每個子群組的中線及管制界限
CLs (s-bar) = $L$2
LCL(n=i) = B3(n=i) * CLs
UCL(n=i) = B4(n=i) * CLs
LCLs = Oi * CLs
→ U4 = O4 * $L$2 = 0 * 0.010 = 0
UCLs = Pi * CLs
→ V4 = P4 * $L$2 = 2.089 * 0.010 = 0.021 - 使用 Excel 畫 圖 #1 所示的兩個管制圖
| 方程 | Excel |
|---|---|
 |
這使用 n (Γn) 的 gamma 函數
使用 Excel 工作表為例,將每個子群組的資料排成一列,如 A1…F1…,當作第一個子群組; A2…F2…當作第二個子群組等。以第一個子群組為例,子群組的樣本數 n 輸入在 Excel 工作表的 A1 計算子群組的 {C4} 公式如下: 在 2003 年版的 Excel,能夠使用 gammaln 的指數 factor {C4}(n=i) = EXP(GAMMALN(A1 / 2)) * SQRT(2 / (A1 - 1)) / EXP(GAMMALN((A1 - 1) / 2)) 從2013年版的 Excel,能夠直接叫出 gamma 函數,即為GAMMA(x) = Γ(x) factor {C4}(n=i) = GAMMA(A1 / 2) * SQRT(2 / (A1 - 1)) / GAMMA((A1 - 1) / 2)) 如果資訊工程師要在 *.net 程式中應用,則利用以下程式 Γ(x) = Chart1. DataManipulator. Statistics. GammaFunction (x) |
 |
繼續利用目前子群組樣本數 n (Excel工作表的 A1)以及在同一列所算出來的 {C4} 的值計算 A3
factor {A3} = 3 / ({C4}(n=i) * SQRT(A1)) |
 |
下一步,標準差的算法說明於下:
{standard-deviation}=3*SQRT(1 - POWER({C4}(n=i), 2)) / {C4} 接著計算因子 {B3},使用剛剛計算的標準差,並確保沒有其結果不小於零。 factor {B3} = IF((1 - {standard-deviation}) < 0, 0, (1 - {standard-deviation})) |
 |
最後,計算 {B4},說明於下:
factor {B4} = 1 +{standard-deviation} |
| n | C4 | A3 | B3 | B4 |
|---|---|---|---|---|
| 2 | 0.7979 | 2.659 | 0.000 | 3.267 |
| 3 | 0.8862 | 1.954 | 0.000 | 2.568 |
| 4 | 0.9213 | 1.628 | 0.000 | 2.266 |
| 5 | 0.9400 | 1.427 | 0.000 | 2.089 |
| 6 | 0.9515 | 1.287 | 0.030 | 1.970 |
| 7 | 0.9594 | 1.182 | 0.118 | 1.882 |
| 8 | 0.9650 | 1.099 | 0.185 | 1.815 |
| 9 | 0.9693 | 1.032 | 0.239 | 1.761 |
| 10 | 0.9727 | 0.975 | 0.284 | 1.716 |
| 11 | 0.9754 | 0.927 | 0.321 | 1.679 |
| 12 | 0.9776 | 0.886 | 0.354 | 1.646 |
| 13 | 0.9794 | 0.850 | 0.382 | 1.618 |
| 14 | 0.9810 | 0.817 | 0.406 | 1.594 |
| 15 | 0.9823 | 0.789 | 0.428 | 1.572 |
| 16 | 0.9835 | 0.763 | 0.448 | 1.552 |
| 17 | 0.9845 | 0.739 | 0.466 | 1.534 |
| 18 | 0.9854 | 0.718 | 0.482 | 1.518 |
| 19 | 0.9862 | 0.698 | 0.497 | 1.503 |
| 20 | 0.9869 | 0.680 | 0.510 | 1.490 |
| 21 | 0.9876 | 0.663 | 0.523 | 1.477 |
| 22 | 0.9882 | 0.647 | 0.534 | 1.466 |
| 23 | 0.9887 | 0.633 | 0.545 | 1.455 |
| 24 | 0.9892 | 0.619 | 0.555 | 1.445 |
| 25 | 0.9896 | 0.606 | 0.565 | 1.435 |
| … | … | … | … | … |
| 50 | 0.9949 | 0.426 | 0.696 | 1.304 |
| … | … | … | … | … |
| 100 | 0.9975 | 0.301 | 0.787 | 1.213 |
關鍵文獻
- Montgomery DC. 1997 Introduction to statistical quality control 3rd edition. John Wiley & Sons Inc. New York. [eng.sut.ac.th]
- C4 Function. Computes the expected value of the standard deviation of n independent normal random variables. [v8doc.sas.com]
- Zaiontz C. Gamma function in Excel. [www.real-statistics.com]
- Microsoft Datavisualization Charting. StatisticFormula.GammaFunction Method. [msdn.microsoft.com/library]