類似於累積和管制圖,指數加權移動平均管制圖對於偵測流程平均值微小的偏移相當有用。指數加權移動平均管制圖的功用大致與累積和管制圖相同,且在某些方面,較容易設定及操作。這些圖示用來監測依流程收集頻率(小時、班、日、周、月等)所取得的樣本所算出的平均值。這些收集頻率樣本的測量值會形成〝次群組〞每個點會依據以往的資料進行加權,但最近的點被給予更多的權重。相對於累積和管制圖,指數加權移動平均管制圖是使用個別的觀察值(但也能夠使用合理次群組的樣本數 n > 1)。另一個選擇是利用 I-型管制圖。 [I-型圖]
指數加權移動平均管制圖仰賴目標值及標準差。由於這個理由,流程管制後,最好是用來尋找目標值的早期偏差。一旦平均值及標準差的估計可以取得,指數加權移動平均管制圖及累積和管制圖對於偵測流程平均值微小的偏移相當有效。
指數加權移動平均的運算
指數加權移動平均值定義為
當 0 ≤ λ ≤ 1 是一個持續的且起始值(所需的樣本為 i = 1) 為流程目標值,為 `z_0 = mu_0`。有時,初步的平均值數據會使用指數加權平均值做為起始值,為 `z_0 = bar x`。指數加權平均管制圖是由 `z_i` 及樣本數 i (或時間)所構成。中線及管制界線,中線 (CL) = `mu_0`,管制界線為
λ為使用者指定且 0.05 ≤ λ ≤ 0.25 區間所定義的,λ = 0.05、 λ = 0.10、 λ = 0.20 為最常選擇的。雖然當λ很小,但使用 L = 3 (代表常用的 3 個標準差的界線)是合理的,λ ≤ 0.1,利用 L 介於 2.6 和 2.8,降低界線的寬度。使用λ= 0.1及 L = 2.7應該會得到控制中的ARL0 ≅ 500的ARL,且為了偵測流程平均值一個標準差的偏移。對於 0.2及 L=3,這會出現異常的訊號,樣本數為 11,有 1σ 偏移。界線的值會依據每個連續的次群組而改變,但但往往在大約十次群組平穩。
合理次群組
目標平均值也許可以直接輸入,或可利用一系列的次群組進行估計。如果是利用次群組進行估計,總均值的公式為
當樣本數的大小隨次群組而變化,建議用加權的方法估計標準差。
如果合理次群組的樣本數 n>1,接著,以 `bar x_i` 取代`x_i` ,以`sigma_(bar x) = sigma / sqrt(n)`取代 `sigma`。
EWMA 示範 (n=1)
資料
流程目標值是 10.0 與 `sigma` = 1。
9.45 7.99 9.29 11.66 12.16 10.18 8.04 11.46 9.20 10.34
9.03 11.47 10.51 9.40 10.08 9.37 10.62 10.31 8.52 10.84
10.90 9.33 12.29 11.50 10.60 11.08 10.38 11.62 11.31 10.52
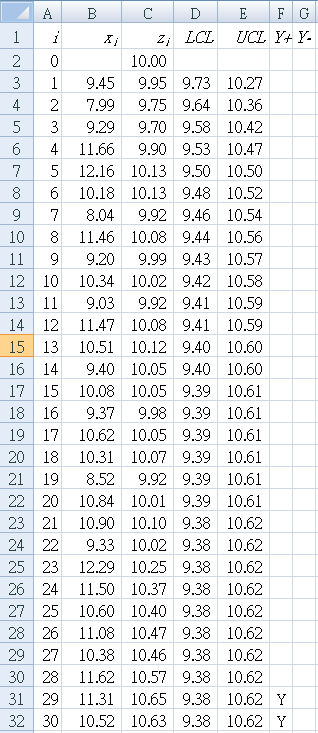
完成表 1 的步驟
B1 : "xi " (每個樣本的數值)
C1 : "zi " (使用上述的公式計算累積和)
D1 : "LCL " (管制下限)
E1 : "UCL " (管制上限)
F1 : "Y+ " (如果 EWMA 值超過 UCL,Y=yes )
G1 : "Y- " (如果 EWMA值低於 LCL,Y=yes )
A3 : "=A2+1"
選擇 A3 單元格,向下拖動(複製公式)直到 A22 為止 …
A32 : "=A30+1"
確認你的採樣序列從 A2:A32 為 0~30。
 A34 : "`bar x`", B34 : "10.00"
A34 : "`bar x`", B34 : "10.00"
A35 : "`sigma`", B35 : "1.0"
A36 : "`lambda`", B36 : "0.1"
A37 : "L", B37 : "2.7"
選擇 C3 單元格,向下拖動(複製公式)直到 C32 為止 …
C32: "=B32*$B$36+(1-$B$36)*C31"
E3: "=$B$34-$B$37*$B$35*SQRT(($B$36/(2-$B$36))*(1-POWER((1-$B$36),(2*A3))))"
選擇 D3 及 E3 單元格,向下拖動(複製公式)直到 E32 為止 …
D32: "=$B$34+$B$37*$B$35*SQRT(($B$36/(2-$B$36))*(1-POWER((1-$B$36),(2*A32))))"
E32: "=$B$34-$B$37*$B$35*SQRT(($B$36/(2-$B$36))*(1-POWER((1-$B$36),(2*A32))))"
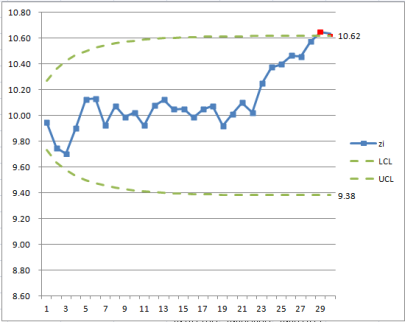
確認你的結果如表 1 的 LCL 及UCL 相同。
G3: "=IF(C3<=D3,"Y","")"
Select F3 together with G3, then drag (copy formula) through to G32 so that …
F32: "=IF(C32>E32,"Y","")"
G32: "=IF(C32<=D32,"Y","")"
Check that your result is a "Y" in cell F31 and F32.
合理次群組 (n>1)
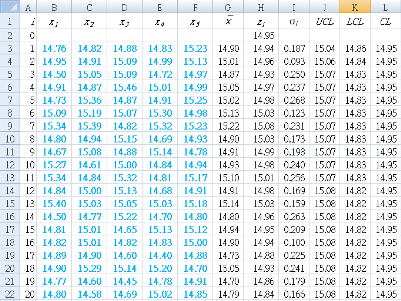
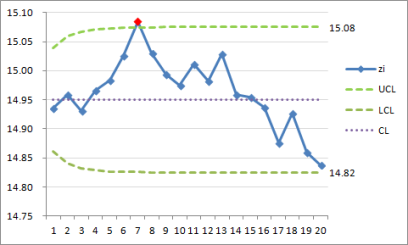
為了監視過程的平均變化,每一天採出五個樣品。以下資料中的每行表示一天的五個採樣點。監測開始於第一行,並繼續進行 20 天(資料的最後一行)。(用戶定義的參數在計算中使用的 λ = 0.3 和 L = 1.5)。
資料
14.76 14.82 14.88 14.83 15.23
14.95 14.91 15.09 14.99 15.13
14.50 15.05 15.09 14.72 14.97
14.91 14.87 15.46 15.01 14.99
14.73 15.36 14.87 14.91 15.25
15.09 15.19 15.07 15.30 14.98
15.34 15.39 14.82 15.32 15.23
14.80 14.94 15.15 14.69 14.93
14.67 15.08 14.88 15.14 14.78
15.27 14.61 15.00 14.84 14.94
15.34 14.84 15.32 14.81 15.17
14.84 15.00 15.13 14.68 14.91
15.40 15.03 15.05 15.03 15.18
14.50 14.77 15.22 14.70 14.80
14.81 15.01 14.65 15.13 15.12
14.82 15.01 14.82 14.83 15.00
14.89 14.90 14.60 14.40 14.88
14.90 15.29 15.14 15.20 14.70
14.77 14.60 14.45 14.78 14.91
14.80 14.58 14.69 15.02 14.85
B1 : "x1 " (第一個採樣的)
C1 : "x2 " (第二個採樣的)
D1 : "x3 " (第三個採樣的)
E1 : "x4 " (第四個採樣的)
F1 : "x5 " (第五個採樣的)
G1 : "`bar x`" (次組的平均)
H1 : "zi " (次組的EWMA值)
I1 : "σi " (次組的標準差值)
J1 : "UCL " (次組的標準差值)
K1 : "UCL " (管制下限)
L1 : "CL " (中線)
A2 : "0"
A3 : "=A2+1"
選擇 A3 單元格,向下拖動(複製公式)直到 A22 為止 …
A22 : "=A21+1"
確認你的採樣序列號從 A2:A22 為 0~20。
選擇 G3 單元格,向下拖動(複製公式)直到 G22 為止 …
G22 : "=AVERAGE(B22:F22)"
確認你的結果是相同如表 2。
選擇 I3 單元格,向下拖動(複製公式)直到 I22 為止 …
I22 : "=STDEV(B22:F22)"
確認你的結果是相同如表 2。
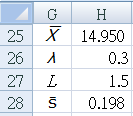
G25 : "`bar bar x`" 所有次組的加權平均
G26 : "`lambda`" 用戶自定
G27 : "L" 用戶自定
G28 : "`bar bar S`" 所有次組的平均標準偏差
H28 : "=AVERAGE($I$3:$I$22)"
選擇 H3 單元格,向下拖動(複製公式)直到 H22 為止 …
H22 : "=$H$26*G3+(1-$H$26)*H21"
確認你的結果是相同如表 2。
選擇 J3 及 K3 單元格,向下拖動(複製公式)直到 K22 為止 …
K22 : "=$H$2-$H$27*$H$28*SQRT(($H$26/(2-$H$26))*(1-POWER((1-$H$26),(2*A22))))"
確認你的結果是相同如表 2。
選擇 L3 單元格,向下拖動(複製公式)直到 L22
樣本大小不一致
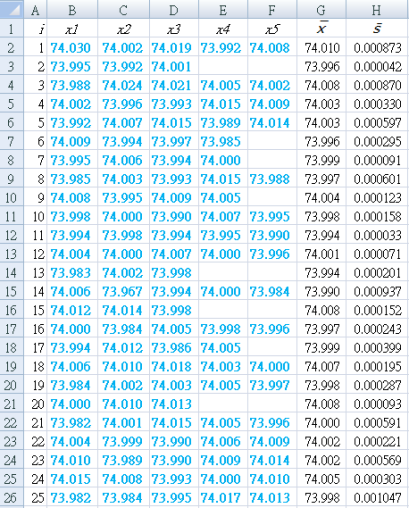
樣本大小不一致的時候,也使用相同的 Excel 公式來計算子組的平均值的加權平均。
`bar bar x` = 74.001
但計算子組的標準偏差的加權平均(H28),公式
`hat sigma = bar s = [(sum_(i=1)^k ((n_i - 1) s_i^2)) / ((sum_(i=1)^k n_i) - k) ]^(1/2)`
可以通過標準差的 Excel 公式中列 H 改變來計算:
選擇 H3 單元格,向下拖動(複製公式)直到 H26
這之後, 計算子組的標準偏差的加權平均 `bar S`, 把 H28 的 Excel 公式改為
`bar S` = 0.01029
UCL 和 LCL 的 Excel 公式不需要修改。它們的值將顯示這些修改的影響。