在滿意度調查分析中常用的統計功能

組資料和Excel功能的用途以協助小樣本調查手工計算

李克特項調查視為常態分配

對於某件事情的主觀評估，無法客觀的衡量，如病人滿意度，此為序位類型的資料型態。舉例來說，病人也許分類其滿意程度為非常不滿意/不滿意/中立/滿意/非常滿意或評估他們的疼痛程度為很小/中度/重度/無法忍受。此種類型的資料也稱為〝序位〞資料。

針對序位資料，我們不能說〝有點滿意〞是〝有點不滿意〞兩倍好，或各個程度間的差異是一樣的(舉例來說，從非常不滿意到有點不滿意和從有點滿意到非常滿意相較)。 當序位類別的資料，如滿意度調查的李克特式尺度，應抵制將這些數字當成有統計意義。 舉例來說，對於計算滿意度平均不夠敏感。這些資訊僅包含序位的資訊母數方法是依據計算平均及標準差，所以他們不適用於序位的資料，如滿意度。 (Altman [1] p.180)

話雖如此，使用Google搜尋，傳回很多以平均值及標準差計算滿意度調查的結果(如美國Press-Ganey調查)。且因我們醫院報給醫務管理學會，要求使用滿意度五分法的平均，我們網頁提供這些計算方法於下。

實例

對調查問卷中的一個項目進行分析，填答者從五分法中選擇1~5中一個，該細項的結果為：

	{4, 5, 4, 5, 5, 5, 5, 3, 4, 3}
表一、使用 Excel 函數由原始數據計算
統計參數 Excel 函數 結果
算術平均值 = AVERAGE(4, 5, 4, 5, 5, 5, 5, 3, 4, 3) = 4.3
標準偏差 = STDEV(4, 5, 4, 5, 5, 5, 5, 3, 4, 3) = 0.823273
樣本數 = COUNT(4, 5, 4, 5, 5, 5, 5, 3, 4, 3) = 10
信賴區間 = CONFIDENCE(0.05, STDEV(), COUNT())  
= CONFIDENCE(0.05, 0.823273, 10) = 0.51027

然而，因為我們的網頁呈現群組的調查資料，這個區塊呈現群組資料給予相同分數的結果如何？

表二、使用 Excel 函數由分組數據計算
從調查的分組數據 計算
A B C D E F G H I J K
1 李克特分數 u 1 2 3 4 5 Σ    
2 投票率 f 0 0 2 3 5 =SUM(D2:H2) 10 =Σf
3 分組數據 fu 2 0 0 18 48 125 =SUM(D3:H3) 191 =Σfu 2
4 分組數據 fu 0 0 6 12 25 =SUM(D4:H4) 43 =Σfu
使用分組的數據來計算統計參數：
樣本標準差 `s`:
` = c \times sqrt ((Sigma f u^2)/(Sigma f) - ((Sigma f u)/(Sigma f))^2) \times sqrt ((Sigma f) / ((Sigma f - 1))) `
` = 1 \times sqrt ((191 / 10) - (43 / 10)^2) \times sqrt (10/((10 - 1))) `
`= 0.781025 \times 1.054093`
`= 0.823273`
與表1其中所用的原始數據計算的結果相同
⇒ STDEV(4, 5, 4, 5, 5, 5, 5, 3, 4, 3)
算術平均值 `bar x`:
` = (Sigma f u)/(Sigma f) `
` = (43 / 10) `
`= 4.3 `
`= 0.823273`
與表1其中所用的原始數據計算的結果相同
⇒ AVERAGE(4, 5, 4, 5, 5, 5, 5, 3, 4, 3)
信賴區間 `CI`:
` = bar x ± z_c s/sqrt(N) `
` = (Sigma f u)/(Sigma f) ± z_c s/sqrt(Sigma f) `
` = 43 / 10 ± 1.96 0.823273/sqrt(10) `
`= 4.3±0.51027 `
與表1其中所用的原始數據計算的結果相同
⇒ CONFIDENCE(0.5, 0.823273, 10)
`= 4.3 ` `(3.78973 ∼ 4.81027)`

或作為5的最大李克特量表的百分比
`= 4.3/5 (3.78973/5 ∼ 4.81027/5)`
`= 86.0% (75.8% ∼ 96.2%)`

信賴區間

信賴區間是一個範圍，用來說明點估計的不確定性（如滿意度），及資料變異性的測量。信賴區間是用機率來計算（如 95%），且我們會說有 95% 的機會，信賴區間會涵蓋真正的數值。 因為統計檢定常定在 0.05，所以絕大多數的信賴區間皆以 95% 計算之，換句話說，只不過是因為〝大家這麼做〞而已。 這是很武斷的：在偶然情況下，100 次中有 5 次例外被當作有統計上的顯著差異，但發生 6 次例外就不算統計上有顯著差異！ 信賴區間未考量點估計不確定性的其他來源，包括遺漏值、資料不完整、其他數據錯誤或由未填答者以及不好的數據收集過程造成的偏差。

常態分配

在 np 和 n(1-p) 都大於 5 的條件下近似常態是合理的，因此僅適用於大樣本（> 30）；但是員工滿意度調查的回收率，或任何滿意度調查的層別法分析，通常會落在此值之下；在這種情況下，建議使用累積較長期的資料﹝如：半年或一年﹞ 舉例來說，如果 `hat p` = 0.1，那 N 應至少要 50，若 `hat p` = 0.01，那N至少要 500。 在其他地方討論了 選擇樣本量 以確保檢測到變化，且當使用管制圖的時候，這是很重要的。

在此公式中，`hat p` 是由統計樣本估計出來的比例，n 是樣本數，z(1-α/2) 是標準常態分布的 (1-α/2) 百分位數（以 95% 信賴區間來說，這個值為 1.96 。當 np及 n(1-p) 都大於 5 的時候，用常態近似法是合理的，因此，他只適用於大樣本的資料 (≥ 30)； 然而，像員工滿意度調查的回收率或任何調查的分層分析，其樣本數往往會在這個標準之下 (n < 30)。

在很多單純的情況下，特別是牽涉到常態分布的資料，或其他分布的大樣本資料，常態估計也許會被用來計算信賴區間。計算方式使用近似常態二項分配算得調查比例的標準誤差：

` hat p ± z_(1 - \alpha \/2) sqrt ((hat p (1 - hat p))/n) `

p-hat 是統計樣本的抽樣比例，n 是樣本數， ` z_(1 - \alpha \/2) ` 是標準常態分配的 1-α/2 百分位 ﹝例如本網站使用的 95% 信賴區間值是 1.96﹞。

計算常態分配的信賴區間的實例

卓越指標：一共有 86 人填表，其中 33 人給四分、12 人給滿分五分。

因此，卓越指標之分子為 33 + 12 = 45、其分母為 86，

p = 45 ÷ 86 = 0.523

1-p = 0.477

n = 86

且使用近似常態二項分配算得需要 np 和 n(1-p) 都 > 5，因此：

np = 86 x 0.523 = 44.978

n(1-p) = 86 x (1-0.523) = 41.02

確實兩個都 > 5。

依據上述的公式， 95% CI
` = 0.523 ± 1.96 sqrt((0.523 × 0.477) / 86) `
` = 0.523 ± 0.105 `

卓越指標 = 52.3% ﹝下限：41.8%, 上線：62.9%﹞或解釋時該說其範圍為 41.8% ~ 62.9% 之間。

我們滿意度調查結果的網頁最右邊兩個欄位是95%信賴區間。


二項式分配

過去，很多分析師建議當樣本數很小的時候，直接從二項式分布算〝精確的〞信賴區間。 然而，精確的信賴區間容易變的太寬。 Agresti & Coull [6] 指出分數的間隔幾乎在所有情況下都比精確的間隔好，即使是樣本數很小的時候。 因此，建議指出分數的間隔適合所有樣本大小的資料，因此此網站的滿意度調查使用使用此種方法。

對二項式分布的資料來說，會利用二次方程式以分數的間隔來計算信賴區間：

` hat p = ((2nx + z_(\alpha \/ 2)^2 n ) ± sqrt(((2nx + z_(\alpha \/ 2)^2 n)^2 - 4 (n^2 + z_(\alpha \/ 2)^2 n) x^2)) ) / (2 ( n^2 + z_(\alpha \/ 2)^2 n )) `
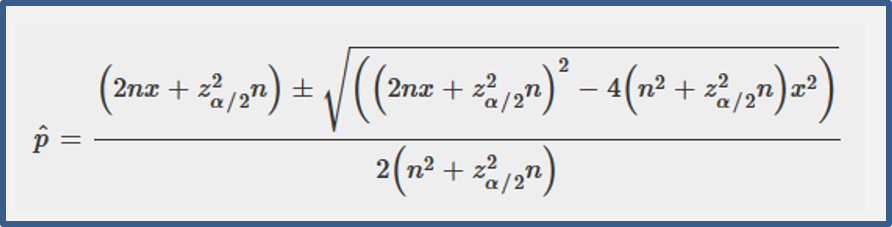
quadratic equation

在此式中，n 是樣本數，x 是成功的數量，zα/2 是α/2 程度的常態離散 (如：1.96 對 95% 的間隔)，且 `hat p`是估計的信心水準。

利用此種方法，下限不會是負值，但是若使用二項分布的常態近似法將不會有這樣的效果。

除非 p ≅ 0.5，否則二項分布的信賴區間並不是對稱的。

計算二項式分配信賴區間的實例

上雙盒指標：一共有 20 人填表，其中 3 人給四分、1 人給滿分五分。

因此，上雙盒指標之分子﹝x﹞為 3 + 1 = 4、其分母﹝n﹞為 20， ` hat p ` = x ÷ n = 4 ÷ 20 = 0.2 (20%)

依據上述的公式： 95% CI

` = ((2nx + z_(\alpha \/ 2)^2 n) ± sqrt(((2nx + z_(\alpha \/ 2)^2 n)^2 - 4 (n^2 + z_(\alpha \/ 2)^2 n) x^2)) ) / (2 ( n^2 + z_(\alpha \/ 2)^2 n )) `
 
` = (2 × 20 × 4 + 1.96^2 × 20 ± sqrt((2 × 20 × 4 + 1.96^2 × 20)^2 - 4 × (20^2 + 1.96^2 × 20 ) × 4^2)) / (2 × ( 20^2 + 1.96^2 × 20 )) `
 
` = (160 + 76.832 ± sqrt((160 + 76.832)^2 - 4 × (400 + 76.832 ) × 16)) / (2 × ( 400 + 76.832 )) `
 
` = (236.832 ± sqrt(56089.39622 - 30517.248)) / 953.664 `
 
` = (236.832 ± 159.9129395) / 953.664 `
 
` UCL = (396.7449395) / 953.664 = 0.416021722 `
 
` LCL = (76.91906049) / 953.664 = 0.080656353 `

依據上述的公式，上雙盒指標 = 20.0% ﹝下限：8.1%, 上線：41.6%﹞或解釋時該說其範圍為 8.1% ~ 41.6% 之間。須注意的是這個結果距平均值是不對稱的，與平均值的距離下限為11.9%，上限為 21.6%。

圖八、患者滿意度的單變量分析
Lights
圖八顯示單因素分析，患者滿意度參數均為非常態分佈，通常偏向左。
圖九、常態和二項計算的比較
Lights
圖九示出信賴區間根據常態和二項式分佈計算的比較。當在進行短期、小範圍、小樣本數的品質改進（PDSA）專案時，這是特別重要的。在這種情況下，圖九的左半邊表明，使用常態近似計算將導致不可能的結果（小於零的信賴區間或大於100％）。圖九的右半部分錶示二項式計算是總是正的，永不超過100％，並且兩側的長度不等。

使用 Excel 計算

1. 在新的工作表,建立實驗的變量,如下:
A1 : "α "        B1: "1.96"
95% CI （如果需要改變為其他值）
A2 : "n "        B2: "20"
有效問卷的總張數（分母）
A3 : "x "        B3: "4"
給出所期待的意見，如頂雙盒（分子）
2. 在工作​​表中的不同格子利用函數設置二項式置信區間的公式，如下：
UCL : " =(2 * $B$2 * $B$3 + POWER($B$1, 2) * $B$2 + SQRT(POWER(2 * $B$2 * $B$3 + POWER($B$1, 2) * $B$2, 2) - 4 * (POWER($B$2, 2) + POWER($B$1, 2) * $B$2) * POWER($B$3, 2))) / (2 * (POWER($B$2, 2) + POWER($B$1, 2) * $B$2)) "
LCL : " =(2 * $B$2 * $B$3 + POWER($B$1, 2) * $B$2 - SQRT(POWER(2 * $B$2 * $B$3 + POWER($B$1, 2) * $B$2, 2) - 4 * (POWER($B$2, 2) + POWER($B$1, 2) * $B$2) * POWER($B$3, 2))) / (2 * (POWER($B$2, 2) + POWER($B$1, 2) * $B$2)) "
3. 結果應該是與上述的實例一樣的，如下所示（如果沒有，請檢查您複製的公式）：
UCL : 0.416021722
LCL : 0.080656353

關鍵文獻

  1. Altman DG. Practical statistics for medical research. Chapman & Hall/CRC, 1991. pp.231-2
  2. Spiegel MR. Shaum's outline of theory and problems of statistics. McGraw-Hill Inc. 1972. p.78-9 section 4.16
  3. Pezzullo JC. Online calculator for Exact Binomial and Poisson Confidence Intervals statpages.org/confint.html
  4. Bhaskar. Online calculator for Mean & Standard Deviation from frequency table & grouped data: knowpapa.com/sd-freq/
  5. Vollset SE. Confidence intervals for a binomial proportion. Statistics in Medicine 1993; 12(9): 809-823.
  6. Agresti A & Coull BA. Approximate is better than "exact" for interval estimation of binomial proportions, The American Statistician, 1998; 52(2): 119-126.